Гиперзвуковые течения газов

§ 1. Изменение параметров газа в изоэнтропическом гиперзвуковом потоке

Течения газа со скоростью, значительно превосходящей скорость звука, называемые иногда гиперзвуковыми течениями, обладают рядом отличительных особенностей.

Выразим в явном виде влияние изменения скорости течения

на основные параметры газа.

В единичной струйке газа при отсутствии потерь и внешней работы, согласно уравнению Бернулли, имеем

.

Отсюда с помощью известного выражения для скорости звука получаем соотношение, связывающее изменение давления с изменением скорости,

(1)

Уравнение сохранения теплосодержания струйки при адиабатическом течении можно представить в виде

После несложных преобразований отсюда следует

(2)

Дифференцируя уравнение состояния идеального газа и используя предыдущие соотношения, получаем аналогичную зависимость для изменения плотности

(3)

Дифференцируя равенство и выражая скорость звука через температуру газа, находим соотношение

. (4)

Соотношения (1)—(4) показывают, что при дозвуковых скоростях (М<1) происходит незначительное изменение давления, плотности и температуры газа с изменением скорости, а число Маха зависит от скорости линейно. Наоборот, при гиперзвуковых скоростях ( ) даже небольшое изменение скорости течения ведет к заметному изменению состояния газа и числа Маха.

При в правой части выражения (4) можно пренебречь единицей, тогда имеем

(5)

Исключая из (1) и (5) множитель и выполняя интегрирование, получаем характерную для гиперзвуковых течений зависимость давления от числа Маха

го ряда был отброшены. 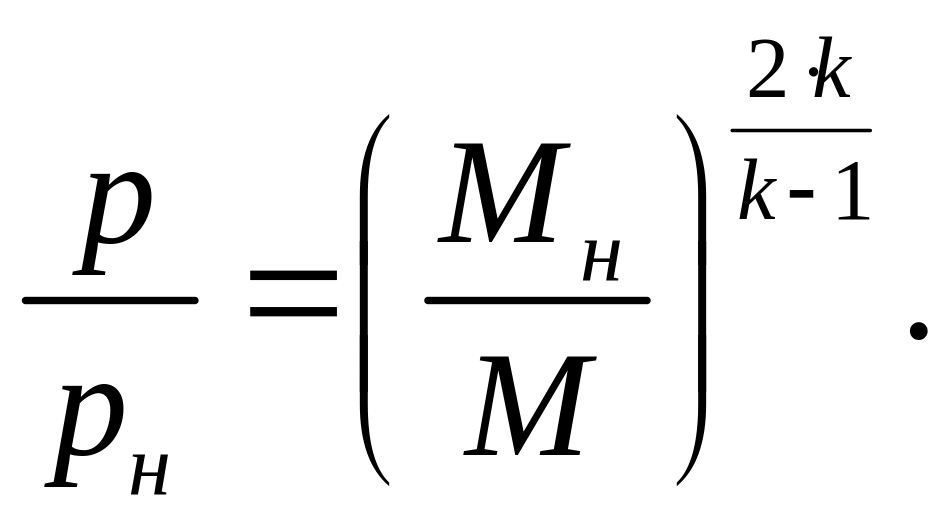(6)

Из (2) и (5) аналогичным путем выводится зависимость температуры от числа Маха

(7)

откуда следуют соответствующие выражения для скорости звука

(8)

и плотности газа

(9)

Интегрируя выражение (5), устанавливаем связь между скоростью потока и числом Маха

(10)

При выводе уравнения (10) функция была разложена в ряд по степеням , причем ввиду близости отношения к единице все нелинейные члены это

В выражениях (6)—(10) величины без индексов соответствуют текущим значениям параметров газа, а величины с индексом «н» - их начальным значениям.