
- •Глава 1. Двойные интегралы
- •§1. Определение двойного интеграла и критерий интегрируемости
- •Определение двойного интеграла
- •Критерий интегрируемости
- •§2. Свойства двойных интегралов
- •3. Вычисление двойных интегралов
- •3.1. Вычисление двойного интеграла сведением к повторному
- •§4. Замена переменных в двойном интеграле
- •§5. Переход к полярным координатам. Вычисление
- •Глава 2. Тройные интегралы
- •Глава 3.Криволинейные интегралы
- •§1. Криволинейные интегралы первого типа
- •§2. Криволинейные интегралы второго типа
- •§3. Формула Грина
- •§4.Независимость криволинейного интеграла от формы пути интегрирования
- •Если всюду в выполнено равенство , то по формуле Грина .
- •§5. Связь с вопросом о полном дифференциале
- •Глава 4. Поверхностные интегралы
- •§1. Площадь поверхности, заданной явным уравнением
- •§2. Площадь поверхности, заданной параметрическими уравнениями
- •§3. Поверхностные интегралы 1-го типа
- •§4. Поверхностные интегралы 2-го типа
- •4.1. Понятие стороны поверхности
- •4. 2.Поверхностные интегралы II типа (II рода)
- •§5. Формула Остроградского-Гаусса
- •§6. Формула Стокса
- •Глава 5. Приложения кратных, криволинейных и поверхностных интегралов. Элементы теории поля
- •§1. Скалярное и векторное поле
- •§2. Производная скалярного поля по направлению. Градиент скалярного поля
- •§3. Поток вектора через поверхность. Дивергенция векторного поля. Векторная формулировка теоремы Остроградского-Гаусса
- •§4. Соленоидальное поле
- •§3. Циркуляция, ротор. Векторная формулировка теоремы Стокса
- •Общая формула Стокса
- •Предельный переход под знаком интеграла
- •1.Гамма-функция
- •2. Бета-функция
- •3. Формула Стирлинга
3. Вычисление двойных интегралов
3.1. Вычисление двойного интеграла сведением к повторному
Двойной
интеграл – новый объект и мы укажем
способ его вычисления сведением к
повторному вычислению определённого
интеграла. Сначала рассмотрим двойной
интеграл по прямоугольной области
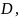 стороны которой параллельны осям
координат.
стороны которой параллельны осям
координат.
Теорема
1.3.
Пусть
для функции
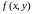 существует двойной интеграл
существует двойной интеграл
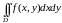 по
области
по
области
 .
Кроме того, пусть для любого
.
Кроме того, пусть для любого
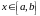 существует
существует
 .
.
Тогда существует и интеграл, называемый повторным:
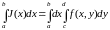
и выполняется равенство
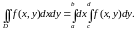 (2)
(2)
►Разобьём
прямоугольник
на прямоугольники, обозначенные
 ,
прямыми, проходящими параллельно оси
,
прямыми, проходящими параллельно оси
 через
точки
через
точки
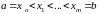 и прямыми, параллельными оси
и прямыми, параллельными оси
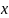 и проходящими через точки
и проходящими через точки
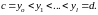 Таким образом,
Таким образом,

Пусть
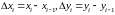 ,
числа
,
числа
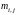 и
и
 ,
соответственно, равны нижней и верхней
граням функции
на
,
соответственно, равны нижней и верхней
граням функции
на
 откуда
откуда
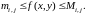 Проинтегрируем эти неравенства по
на
отрезках
Проинтегрируем эти неравенства по
на
отрезках
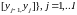 :
:

Суммируя
эти неравенства по
 от
от
 до
до
 ,
получаем.
,
получаем.
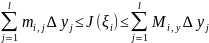
Умножим
все части этих неравенств на
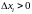 и суммируем полученные неравенства по
и суммируем полученные неравенства по
 от
от
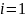 до
до
 :
:
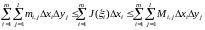 .
.
Поскольку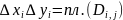 ,
эти неравенства можно переписать в виде
,
эти неравенства можно переписать в виде
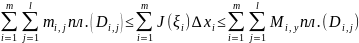
или
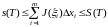 ,
,
где
– разбиение
на прямоугольники
 При
При
 стремится к нулю и величина
стремится к нулю и величина
 .
Кроме того, при
также
.
Кроме того, при
также .
Значит, интеграл
.
Значит, интеграл
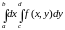 существует и равен
,
что и утверждалось.
◄
существует и равен
,
что и утверждалось.
◄
Замечания.
В случае, когда непрерывна на все условия теоремы выполняются и равенство (2) справедливо.
Сравните эту теорему с теоремой из приложения 1.Отметим, что интеграл представляет собой собственный интеграл, зависящий от параметра.
Рассмотрим случай криволинейной трапеции. Справедлива такая теорема:
Теорема
1.4 (Фубини).
Пусть
область
задана неравенствами

 ,
где
,
где
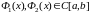 .
Пусть существует
.
Пусть существует
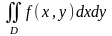 и для любого
существует
и для любого
существует
 .
Тогда существует интеграл
.
Тогда существует интеграл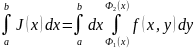 и он равен
.
и он равен
.
►Так
как
 непрерывна на
непрерывна на
 ,
существует её минимальное значение
,
существует её минимальное значение
 на
этом отрезке. Аналогично, существует
мак
на
этом отрезке. Аналогично, существует
мак в прямоугольник
в прямоугольник
 ,
состоящий из точек
,
состоящий из точек
 ,
,
 ,
,
 .
На этом прямоугольнике рассмотрим
функцию
.
На этом прямоугольнике рассмотрим
функцию
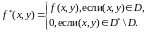
Условия
предыдущей теоремы для функции
 ,
выполнены. Она интегрируема в
,
равна 0 (и, значит, интегрируема) в
,
выполнены. Она интегрируема в
,
равна 0 (и, значит, интегрируема) в
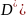 .
Следовательно, она интегрируема на всём
множестве
.
При этом
.
Следовательно, она интегрируема на всём
множестве
.
При этом
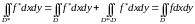 .
.
Наконец,
для любого
 выполнено
равенство
выполнено
равенство
 .
.
По доказанному в предыдущей теореме,
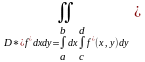 ,
,

Откуда сразу получаем:
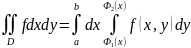 ,
,
что и требовалось доказать.◄
Следствие:
Пусть
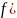 )
непрерывна
в области
,
ограниченной
сверху графиком функции
)
непрерывна
в области
,
ограниченной
сверху графиком функции
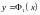 ,
снизу
-
,
где
,
a
по
бокам - отрезками вертикальных прямых
х
= а
и
х
= b.
Тогда
,
снизу
-
,
где
,
a
по
бокам - отрезками вертикальных прямых
х
= а
и
х
= b.
Тогда
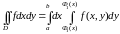 .
.
►Из
непрерывности
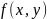 сразу следует её интегрируемость на
.
Кроме того, для любого
сразу следует её интегрируемость на
.
Кроме того, для любого
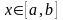 функция
непрерывна (а, значит интегрируема по
у).
Все условия теоремы выполнены.
◄
функция
непрерывна (а, значит интегрируема по
у).
Все условия теоремы выполнены.
◄
Замечание.
Если область
можно ограничить так:
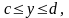
 ,
,
 ,
то
,
то
 .
.
Смысл этих теорем ясен – указан способ сведения двойного интеграла к собственным интегралам, зависящим от параметра.
§4. Замена переменных в двойном интеграле
При
вычислении интегралов часто бывает
удобно сделать замену переменных
 ,
где
,
где – непрерывны в некоторой области
– непрерывны в некоторой области
 .
Впоследствии мы будем часто писать
просто
.
Впоследствии мы будем часто писать
просто
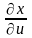 вместо
вместо
 и т.п. и, кроме того, говорить при выполнении
вышеупомянутых условий, что x
и y
– непрерывно дифференцируемые в Δ
функции. Будем также использовать
обозначения
и т.п. и, кроме того, говорить при выполнении
вышеупомянутых условий, что x
и y
– непрерывно дифференцируемые в Δ
функции. Будем также использовать
обозначения
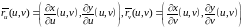 .
.
Пусть
при этом формулы
задают взаимно-однозначное отображение
квадрируемых областей: .
Кроме того, потребуем, чтобы всюду на
области Δ
не равнялся 0 якобиан отображения
.
Кроме того, потребуем, чтобы всюду на
области Δ
не равнялся 0 якобиан отображения
 .
.
Теорема
1.5.
При
сформулированных выше условиях для
непрерывной на
функции
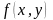 выполняется равенство
выполняется равенство
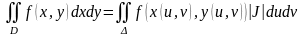 .
.
►Строгое доказательство этой теоремы потребовало бы значительных усилий из-за обилия технических деталей. Мы изложим здесь схему доказательства. Во-первых, оба интеграла в формулировке теоремы существуют, поскольку – непрерывная функция.

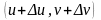
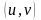

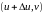

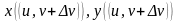
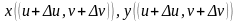



Далее,
при
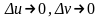
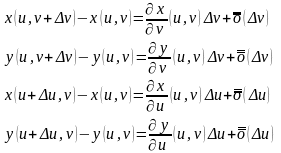
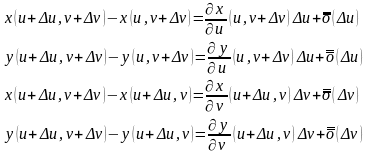
При
малых
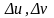 производные
производные
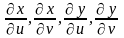 ,
вычисленные в точках
,
вычисленные в точках
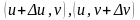 ,
мало отличаются от соответствующих
производных, вычисленных в точке
,
поэтому и определённые выше векторы
,
мало отличаются от соответствующих
производных, вычисленных в точке
,
поэтому и определённые выше векторы
 мало отличаются от векторов
мало отличаются от векторов
 и
и
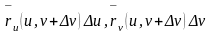 ,
соответственно, и рассматриваемый
четырёхугольник представляет собой
«почти параллелограмм».
,
соответственно, и рассматриваемый
четырёхугольник представляет собой
«почти параллелограмм».
Как
известно из курса линейной алгебры,
площадь параллелограмма со сторонами
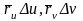

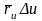
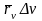
 равна модулю определителя, составленного
из координат этих векторов,
равна модулю определителя, составленного
из координат этих векторов,
 ,
,
т.е
равна
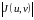
 .
Поэтому при сделанном преобразовании
координат интегральная сумма
.
Поэтому при сделанном преобразовании
координат интегральная сумма

близка по величине к интегральной сумме
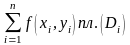 .
.
Точнее говоря, можно доказать, что соответствующие интегральные суммы для интегралов, стоящих в правой и левой частях доказываемого равенства, отличаются друг от друга на стремящуюся к нулю величину. Поэтому и интегралы совпадают.◄
Замечание. Утверждение теоремы сохранится, если условие взаимной однозначности отображения нарушится на множестве нулевой площади.
