1.5 Синтез нелинейных моделей

Примем, что в динамической модели с одной степенью свободы между платформой и корпусом установлен нелинейный упругий элемент, при котором дифференциальное уравнение после гармонической линеаризации и перехода к безразмерному времени 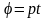имеет вид

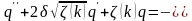(1.5.1)

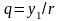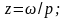
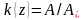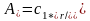
Здесь принято: - безразмерная координата платформы, отсчитываемая от положения статического равновесия; - безразмерная амплитуда; 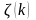-коэффициент гармонической линеаризации.

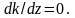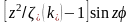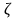Произведём параметрический синтез колебательной системы таким образом, чтобы при отсутствии диссипации выполнять условие Тогда правая часть дифференциального уравнения (1.5.1) равна ; здесь звёздочки при и 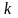отвечают значениям этих параметров согласно уравнению

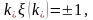(1.5.2)

Полученному пр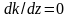и и

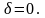
Безразмерная амплитудно-частотная характеристика при учёте (1.5.2) и 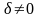приобретает вид

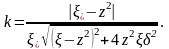(1.5.3)

Зависимость (1.5.3) представим в виде биквадратного уравнения относительно безразмерной частоты

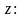
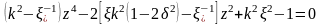. (1.5.4)

При из (1.5.3) следует условие (1.5.2); это свидетельствует о том, что постоянная амплитуда равна статической амплитуде.

Для конкретизации нелинейностей восстанавливающая сила была принята пропорциональной 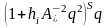, где 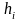- коэффициент пропорциональности; 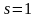- отвечает жёсткой упругой характеристике, а 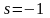- мягкой. При этом имеем

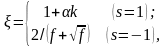(1.5.5)

Где 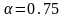; 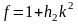. Границам области динамической устойчивости соответствуют уравнения, полученные в [3].

Для жёсткой характеристики

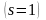
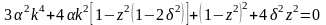. (1.5.6)

Для мягкой характеристики

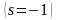
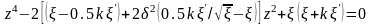, (1.5.7)

Где .

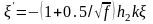Глава 2 Синтез системы виброзащиты на основе методики аналитического конструирования виброзащитных систем в случае детерминированных возмущений

1. Аналитическое конструирование виброзащитных систем.

Рассмотрим линейную систему с постоянными коэффициентами

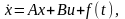(2.1.1)

Где х – n-мерный вектор фазовых координат системы; u – r-мерный вектор управления; B – nxr-матрица; f(t) – n-мерный вектор возмущений.

Предполагаем, что на управление u ограничения не наложены, а возмущения f(t) является непрерывной, ограниченной вектор – функцией времени. Кроме этого предполагается, что система (2.1.1) при 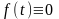является вполне управляемой.

.

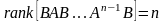Требуется определить u(x,t), доставляющее минимум функционалу

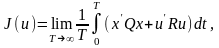(2.1.2)

Где Q – неотрицательно определённая, постоянная nxn – матрица; R – положительно определённая, постоянная rxr – матрица.

Предложенная постановка задачи синтеза регулятора отличается от известной тем, что в качестве возмущения выступают ограниченные неисчезающие на бесконечности функции. В случае ограниченных неисчезающих возмущений при бесконечном интервале наблюдения квадратичный критерий не может служить оценкой качества управления, так как при любом допустимом управлении квадратичный функционал равен бесконечности. Поэтому в качестве оптимизируемого критерия взят среднеквадратичный функционал (2.1.2).

Для данной задачи было получено обобщение метода аналитического конструирования оптимального регулятора, согласно которому при условии вполне управляемости системы при возмущениях f(t) являющихся непрерывной, ограниченной вектор функцией, оптимальное управление u^*(x,t) определяется соотношением

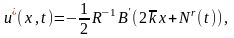(2.1.3)

Где 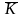симметричное положительно-определённое решение матричного уравнения Рикатти

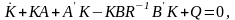(2.1.4)

а n-мерная вектор-функция N^r(t)-частное решение системы

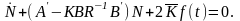(2.1.5)

Пусть система виброзащиты описывается системой уравнений

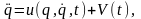(2.1.6)

Где q – n-мерный вектор обобщённых координат, определяющих относительное смещение объекта; V(t) – n-мерная веткор-функция, определяющая внешние возмущения (кинематические или силовые); 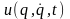- n- мерная вектор функция, определяющая динамическую реакцию виброизолирующего устройства (при решении задачи играет роль управления).

Требуется определить функцию 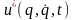, доставляющую минимум функционалу

(2.1.7)

Здесь 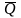и R – положительно определённые nxn – матрицы.

Заметим, что (2.1.6) является вполне управляемой. Введя дополнительные переменные 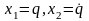приведём (2.1.6) к виду (2.1.1). в этом случае A и B определяются следующим образом:

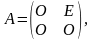
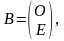
Где E, O- соответственно единичная и нулевая nxn – матрицы.

Для определения воспользуемся изложенным выше. В соответствии с представлением матриц А и В представим входящую в управление (2.1.4) матрицу К в виде

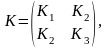(2.1.8)

Где К₁, К₂, К₃ – nxn-матрицы, а частное решение N^r(t)

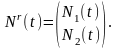(2.1.9)

Здесь N₁(t), N₂(t) –n-мерные вектор-функции.

В силу этих представлений, с учётом того, что в рассматриваемой задаче

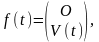
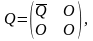
Матричное алгебраическое уравнение Рикатти (2.1.4) разделится на три матричных уравнения

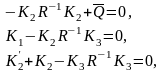(2.1.10)

А система линейных дифференциальных уравнений (2.1.5) запишется следующим образом

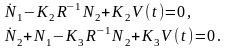(2.1.11)

С учётом введённых разложений матрицы K (2.1.8) и вектор-функции N^r(t) (2.1.9) запишем оптимальное уравнение (2.1.3) в виде

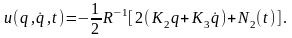(2.1.12)

Таким образом (2.1.12) определяет оптимальную систему виброзащиты, её оптимальную структуру.