
- •Оглавление
- •Глава 1. Виброзащитные системы. Состояние и задачи исследования……5
- •Глава 2. Синтез системы виброзащиты на основе методики аналитического конструирования виброзащитных систем в случае детерминированных возмущений………………………………………………………………………22
- •Введение
- •Глава 1 Виброзащитные системы. Состояние и задачи исследования
- •Проблема виброзащиты
- •Постановка задачи параметрической оптимизации виброзащитной системы
- •1.3 Синтез линейной динамической модели с одной степенью свободы
- •1.4 Синтез линейной динамической модели с двумя степенями свободы
- •1.5 Синтез нелинейных моделей
- •Глава 2 Синтез системы виброзащиты на основе методики аналитического конструирования виброзащитных систем в случае детерминированных возмущений
- •Аналитическое конструирование виброзащитных систем.
- •Синтез виброзащитной системы, содержащей пассивные и активные элементы
- •Частный случай синтеза виброзащитной системы, содержащей пассивные и активные элементы
- •Модельные примеры
- •Заключение
- •Список исполльзованных источников
1.3 Синтез линейной динамической модели с одной степенью свободы
Согласно уравнению
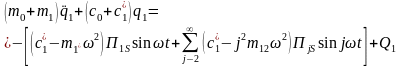 (1.3.1)
(1.3.1)
где
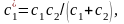
вынужденные колебания описываются зависимостью
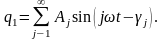 (1.3.2)
(1.3.2)
Здесь
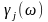 - фазочастотная характеристика,
- фазочастотная характеристика,
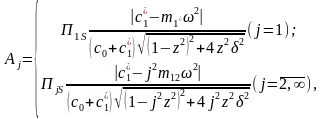 (1.3.3)
(1.3.3)
Где
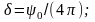
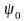 - это коэффициент рассеяния;
- это коэффициент рассеяния;
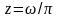 ;
;
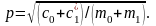
Потребуется, чтобы
при отсутствии диссипации
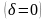 выполнялось
выполнялось
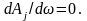 тогда на основании (1.3.3)
тогда на основании (1.3.3)
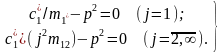 (1.3.4)
(1.3.4)
Условия (1.3.4) не
зависят от ω. Это означает, что
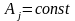 ;
при этом
;
при этом
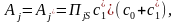 что свидетельствует о нетривиальной
ситуации, когда амплитудно-частотная
характеристика для данной гармоники j
не зависит от частоты возмущения ω. При
учёте линейной силы сопротивления
что свидетельствует о нетривиальной
ситуации, когда амплитудно-частотная
характеристика для данной гармоники j
не зависит от частоты возмущения ω. При
учёте линейной силы сопротивления
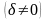 имеем
при резонансном соотношении частот
(jz=1)
парадоксальный результат: соответствующая
«резонансная» амплитуда обращается в
нуль. Физический смысл этого эффекта
связан с частотным совмещением резонанса
с антирезонансом, причём в этом
динамическом конфликте «побеждает»
антирезонанс.
имеем
при резонансном соотношении частот
(jz=1)
парадоксальный результат: соответствующая
«резонансная» амплитуда обращается в
нуль. Физический смысл этого эффекта
связан с частотным совмещением резонанса
с антирезонансом, причём в этом
динамическом конфликте «побеждает»
антирезонанс.
Далее обратимся
к важным приложениям. Если в качестве
циклового механизма выбрать синусный
механизм, то
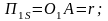
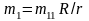 и
и
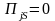 при j>1.
При этом безразмерная амплитудно-частотная
характеристика приобретает вид,
показанный на рис.2. Здесь принято
при j>1.
При этом безразмерная амплитудно-частотная
характеристика приобретает вид,
показанный на рис.2. Здесь принято
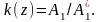 принимая во внимание физическое
происхождение выявленного динамического
эффекта, в резонансной зоне можно ожидать
повышенную чувствительность к точности
частотной настройки. Можно показать,
что при требовании
принимая во внимание физическое
происхождение выявленного динамического
эффекта, в резонансной зоне можно ожидать
повышенную чувствительность к точности
частотной настройки. Можно показать,
что при требовании
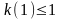 левая часть первого из условий (1.3.4) не
должна превышать по абсолютной величине
левая часть первого из условий (1.3.4) не
должна превышать по абсолютной величине
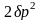 .
.
Для кривошипно-ползунного механизма (рис.1, в) функция положения с достаточной точностью может быть описана бигармонической функцией
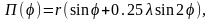
Где r
– радиус кривошипа;
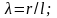 l
– длина шатуна.
l
– длина шатуна.
Потребуем, чтобы
для основной гармоники j=1
удовлетворялось условие (1.3.4). Тогда при
z=1
(ω=p)
имеем
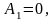 а при
а при
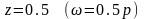 получим
получим
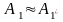 ;
;
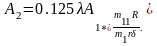 (1.3.5)
(1.3.5)
При этом
предполагается, что масса шатуна
статически размещена между шарнирами
А
и В.
Из (1.3.5) следует, что при уравновешивании
кривошипа (R=0)
на резонансной частоте по второй
гармонике
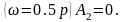
1.4 Синтез линейной динамической модели с двумя степенями свободы
Обратимся к динамической модели с двумя степенями свободы, которой отвечает система дифференциальных уравнений
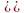 (1.4.1)
(1.4.1)
Не сужая общности в постановке задачи, произведём параметрический синтез колебательной системы с аномальными свойствами для случая моногармонического возбуждения.
При отсутствии диссипации (δ=0) и R=r амплитуда вынужденных колебаний платформы A1 определяется следующим образом:
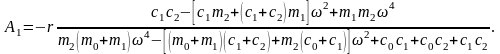 (1.4.2)
(1.4.2)
Введём следующие условные обозначения:
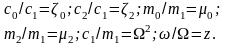
Можно показать,
что
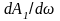 обращается в нуль при
обращается в нуль при
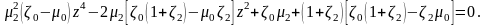 (1.4.3)
(1.4.3)
Условие (9)
свидетельствует о том, что частотный
фактор z
может быть исключён из этого уравнения
лишь при
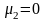 ,
т.е. для системы с одной степенью свободы.
Поэтому в данном случае речь идёт не о
постоянстве амплитуды, а об условии
экстремума. Тем не менее левая часть
условия (1.4.3) характеризует уровень
производной
,
т.е. для системы с одной степенью свободы.
Поэтому в данном случае речь идёт не о
постоянстве амплитуды, а об условии
экстремума. Тем не менее левая часть
условия (1.4.3) характеризует уровень
производной
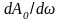 ,
поэтому её малые значения могут быть
использованы для получения квазипостоянных
амплитуд вынужденных колебаний. С этой
целью примем относительно малые значения
,
поэтому её малые значения могут быть
использованы для получения квазипостоянных
амплитуд вынужденных колебаний. С этой
целью примем относительно малые значения
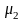 и введём одно из дополнительных требований
вида
и введём одно из дополнительных требований
вида
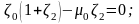 (1.4.4)
(1.4.4)
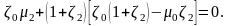 (1.4.5)
(1.4.5)
В первом случае,
отвечающем условию (1.4.4), обращается в
нуль коэффициент при
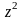 ,
а при условии (1.4.5) – свободный член. Как
показал анализ, с позиции поставленной
задачи более предпочтительным оказывается
условие (11). При этом имеют место два
экстремума – при
,
а при условии (1.4.5) – свободный член. Как
показал анализ, с позиции поставленной
задачи более предпочтительным оказывается
условие (11). При этом имеют место два
экстремума – при
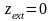 и
и
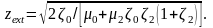
Можно показать, что эти экстремумы являются «слабыми», что проявляется в малых изменениях производной в окрестностях этих значений. Последнее, естественно, свидетельствует о квазипостоянном характере изменения амплитуд.
При соблюдении
условия (1.4.4) и
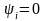
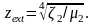 Интересно, что в этом случае амплитуды
вынужденных колебаний при
Интересно, что в этом случае амплитуды
вынужденных колебаний при
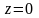 и
и
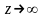 совпадают.
совпадают.
Далее для корректного
учёта частотно независимой диссипации,
характерной для реальных механизмов,
осуществим переход к нормальным
координатам
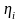 согласно зависимостям
согласно зависимостям
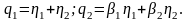 (1.4.6)
(1.4.6)
Здесь
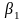 и
и
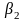 - коэффициенты формы, определяемые как
корни следующего квадратного уравнения
- коэффициенты формы, определяемые как
корни следующего квадратного уравнения
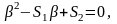
Где
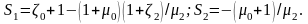
После эквивалентной линеаризации диссипативных сил запишем
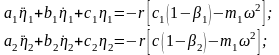 (1.4.7)
(1.4.7)
Где
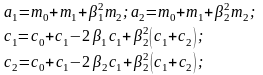
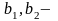 приведение к
соответствующей форме коэффициенты
эквивалентного линейного сопротивления.
приведение к
соответствующей форме коэффициенты
эквивалентного линейного сопротивления.
На основании (1.4.7) амплитуда вынужденных колебаний определяется как
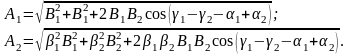 (1.4.8)
(1.4.8)
Здесь
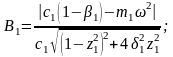
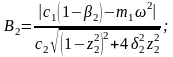

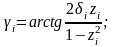
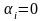 при
при
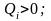
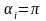 при
при
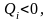
Где
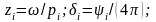
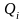 - правая часть
соответствующего уравнения (1.4.7);
- правая часть
соответствующего уравнения (1.4.7);
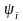 - приведённый коэффициент рассеяния.
- приведённый коэффициент рассеяния.
При необходимости,
как и для модели степенью свободы, в
зоне первого резонанса можно обеспечить
условие A1=0
за счёт параметра
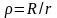 .
.
Анализируя
зависимость (1.4.2), можно убедиться в том,
что при
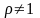 в числителе вместо m1
следует подставить
в числителе вместо m1
следует подставить
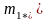 ,
в то время как знаменатель остаётся
неизменным. Это свидетельствует о том,
что параметр ρ влияет лишь на частотную
настройку функции возмущения, не влияя
на значение собственных частот. Потребуем,
чтобы при
,
в то время как знаменатель остаётся
неизменным. Это свидетельствует о том,
что параметр ρ влияет лишь на частотную
настройку функции возмущения, не влияя
на значение собственных частот. Потребуем,
чтобы при
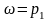 числитель функции (1.4.2)
обратился в нуль. Тогда
числитель функции (1.4.2)
обратился в нуль. Тогда
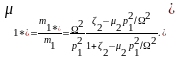 (1.4.9)
(1.4.9)
Принимая во
внимание, что
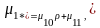 где
где
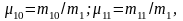 получаем
получаем
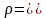 Для принятых исходных данных
Для принятых исходных данных
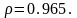 При указанных коррективах амплитуда
вынужденных колебаний при
обращается в нуль.
При указанных коррективах амплитуда
вынужденных колебаний при
обращается в нуль.
