нулевая
.docМИНОБРНАУКИ РОССИИ
ФБГОУ ВПО Рыбинский Государственный Авиационный Технический Университет им. П.А.Соловьева
Кафедра ОиТФ
Факультет: ФАД |
К работе допущен: |
Группа: ЭПБ-11 |
(подпись, дата) |
Работа выполнена: |
|
Студент: |
(лаборант, преподаватель) |
Отчет принят: |
|
Преподаватель: Медведникова Е.В. |
(подпись, дата) |
Рабочий протокол и отчет по лабораторной работе № 0
Знакомство с методами измерения физических величин и оценкой погрешности измерений
(название работы) |
1 Задача: Ознакомиться с прямыми и косвенными измерениями, методами обработки результатов измерений. Провести измерения линейных размеров тел, объёмов, масс, плотностей.
2 Объект и метод исследования: Опытные образцы в виде параллелепипеда 1, цилиндра, параллелепипеда 2, исследуемые (измеряемые) при помощи штангенциркуля и весов. На данных образцах проводятся прямые измерения (линейные размеры тела, масса), а также косвенные измерения, проводимые на основе функциональной зависимости между непосредственно измеряемыми величинами.
3 Рабочие формулы и исходные данные:
Среднее значение рассчитывается по
формуле
.
Объем рассчитывается по формуле V=abs,
используя полученные средние значения.
Абсолютная погрешность прямых измерений
рассчитывается как
,
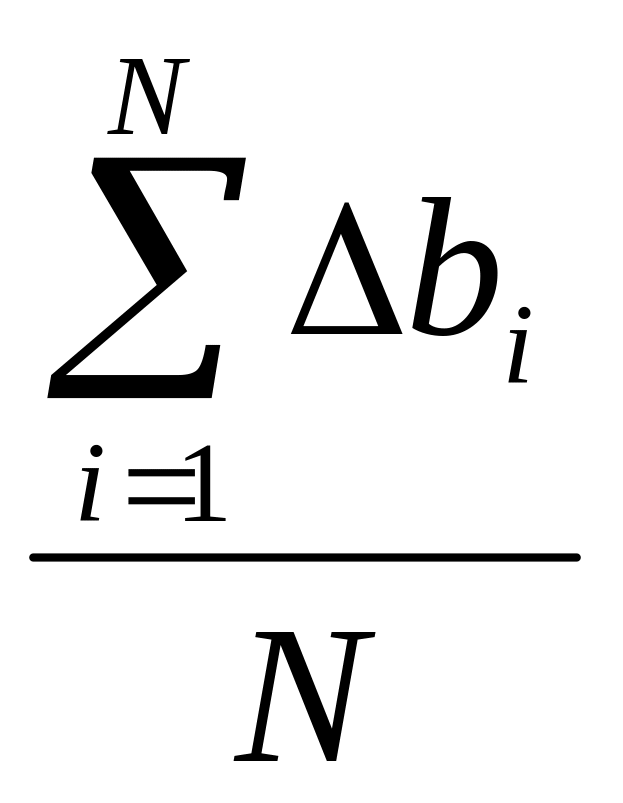где
.
Абсолютная погрешность косвенных измерений, таких как V, рассчитывается как
.
Абсолютная погрешность частного
рассчитывается по формуле
.
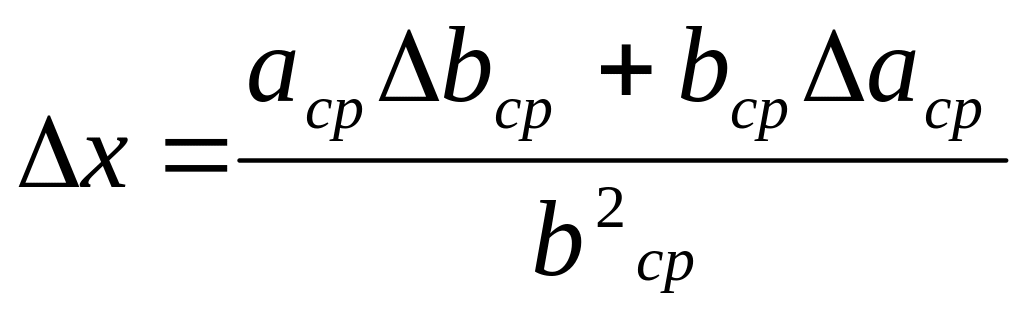Относительную погрешность можно
рассчитать по данной формуле
Параллелепипед
№ |
a, 10-3 м |
b, 10-3 м |
c, 10-3 м |
m, 10-3 кг |
1 |
7.2 |
11.7 |
15 |
9.8 |
2 |
7.1 |
11.76 |
15.1 |
9.5 |
3 |
7.15 |
11.72 |
15.07 |
9.1 |
Цилиндр 1
№ |
a, 10-3 м |
h, 10-3 м |
m, 10-3 кг |
1 |
12.2 |
17.3 |
14.7 |
2 |
12.1 |
16.3 |
14.2 |
3 |
12.4 |
16.6 |
15.1 |
Параллелепипед 2
№ |
a, 10-3 м |
h, 10-3 м |
m, 10-3 кг |
1 |
12,1 |
16,25 |
14,55 |
2 |
12,15 |
16,2 |
14,6 |
3 |
12,1 |
16,25 |
14,65 |
4 Измерительные приборы:
№ п.п. |
Наименование |
Тип прибора |
Используемый предел (диапазон) |
Погрешность прибора или формула погрешности |
1 |
Штангенциркуль |
учебный |
0-0,15м |
0,0005 м |
2 |
Весы |
учебный |
10-4 кг |
0,0005 кг |
5 Результаты измерений и вычислений (Таблицы, примеры расчетов, оценки погрешностей)
Параллелепипед 1
№ опыта |
10 -3 м |
|
|
103 м |
|
,% |
10-3 м |
м |
,% |
10-3 кг |
|
,% |
10 -9 м3 |
|
,% |
|
кг/м3 |
|
1 |
7.2 |
0.05 |
0.69 |
11.7 |
0,03 |
0.26 |
15.0 |
0,05 |
0.03 |
9.8 |
0.33 |
3.37 |
1263.6 |
16,15 |
1,2 |
7755.6 |
254.02 |
3,3 |
2 |
7.1 |
0,05 |
0.70 |
11.76 |
0,06 |
0.51 |
15.1 |
0,05 |
0.033 |
9.5 |
0.03 |
0.32 |
1260.79 |
19.44 |
1,5 |
7534.96 |
272.38 |
3,6 |
3 |
7.15 |
0 |
0 |
11.72 |
0.01 |
0.08 |
15.07 |
0,02 |
0.13 |
9.1 |
0.37 |
4.06 |
1262.83 |
12,37 |
0,9 |
7206.03 |
295.55 |
3,9 |
ср. |
7.15 |
0.05 |
0.699 |
11.73 |
0.033 |
0.28 |
15.05 |
0.04 |
0.27 |
9.47 |
0.243 |
2.5 |
1262.4 |
16,1 |
1,3 |
7501.58 |
295 |
3,5 |
,
,110-3
м
,%
,
10-3
м
,
10-3
10-3
кг
,
10-9,
м3
,
кг/м3
,
,%
Цилиндр
№ опыта |
|
|
,% |
l, 10-3 м |
|
,% |
, 10-3 -кг |
, 10-3 кг |
,% |
, 10-9 м |
, 10-9 м |
,% |
, кг/м3 |
кг/м3 |
,% |
1 |
12,2 |
0,03 |
0.25 |
17.3 |
0.6 |
3.4 |
14.7 |
0,1 |
0.68 |
2021 |
72 |
3,6 |
4800.86 |
115.4 |
2,8 |
2 |
12,1 |
0,13 |
1.07 |
16.3 |
0.4 |
0.025 |
14.2 |
0,4 |
2.81 |
1873 |
66 |
3,3 |
5100.77 |
101.4 |
3,1 |
3 |
12,4 |
0,17 |
1.37 |
16.6 |
0.1 |
0.6 |
15.1 |
0,5 |
3.3 |
2003 |
71 |
3,6 |
4900 |
123,1 |
2,2 |
ср. |
12,23 |
0.33 |
2.7 |
16.7 |
0.36 |
0,29 |
14.6 |
0.34 |
2.3 |
1965 |
69,6 |
3,45 |
4900.8 |
113,3 |
2,7 |
,
10-3
м
,10-3
м
,10-3
м
Параллелепипед 2
№ опыта |
, 10 -3 м |
,10-3 м |
,% |
, 103 м |
10-3 м |
,% |
, 10-3 м |
10-3 м |
,% |
10-3 кг |
10-3 кг |
,% |
, 10 -9 м3 |
10-9, м3 |
,% |
, кг/м3 |
, кг/м3 |
,% |
1 |
23.4 |
0.06 |
0.26 |
8.9 |
0.4 |
4.5 |
24.8 |
0.44 |
1.77 |
6.1 |
0.03 |
0.49 |
5164.8 |
353 |
6 |
1181 |
74 |
6 |
2 |
23.5 |
0,04 |
0.17 |
9.1 |
0.2 |
2.2 |
24.3 |
0.06 |
0.25 |
6.4 |
0.33 |
5.4 |
5196.5 |
129 |
0,3 |
1231 |
31,5 |
2,7 |
3 |
23.47 |
0.01 |
0.04 |
9.9 |
0.6 |
6.06 |
24 |
0,36 |
1.5 |
5.7 |
0.37 |
6.4 |
5576.5 |
445 |
8 |
1022 |
16 |
1,3 |
ср. |
23.46 |
0.036 |
0.15 |
9.3 |
0.4 |
4.3 |
24.36 |
0.287 |
1.18 |
6.07 |
0.24 |
3.95 |
5312.6 |
309 |
4,7 |
1144 |
40 |
3,3 |
Среднее значение
рассчитывается по формуле
,
например найдем aср.
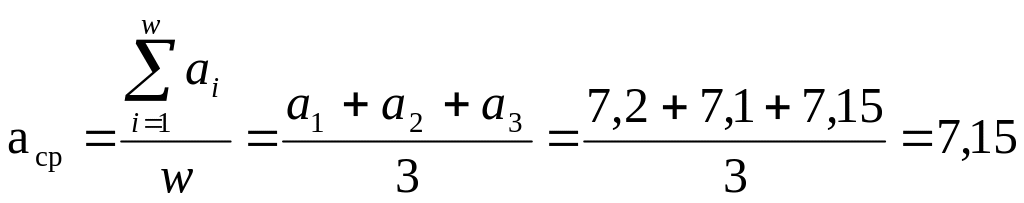, аналогичным способом находятся средние
значения b,
c,
m.
Объем рассчитывается по формуле V=abc
из полученных средних значений. Плотность
рассчитывается по формуле
Абсолютная погрешность прямых измерений рассчитывается как , где . Абсолютная погрешность косвенных измерений, таких как V, рассчитывается как . Абсолютная погрешность частного, таких как плотность, рассчитывается по формуле . Относительную погрешность можно рассчитать по данной формуле .
6 Выводы (Основные результаты работы и их анализ)
На лабораторной работе я ознакомился с прямыми и косвенными измерениями и методами обработки результатов измерений. В лаборатории я провел цепь опытов и применил полученные знания на практике, обрабатывая результаты этих опытов. Также я научился находить абсолютную и относительную погрешность измерений. При любых измерениях нет возможности найти точные значения. Чтобы получить значения максимально близкие к истинным, нужно провести большое число измерений и на их основе вычислить среднее арифметическое значение. Все расчеты проводились с учетом правил приближенных вычислений.
7 Замечания преподавателя, дополнительные задания.