4.10.Структуры данных типа дерева. Основные операции над бинарными деревьями. Решение задачи сортировки с помощью дерева. Примеры программирования операций над деревьями.
Древовидные структуры.
Дерево – это структура, содержащая узел T, с которым связано конечное число древовидных структур с базовым типом T, называемых поддеревьями.
Верхний узел дерева – это корень. Каждый новый узел – это новый уровень дерева и, соответственно, потомок предыдущего узла. Если узел не имеет потомков – он называется листом (терминальный узел).
Элемент, не являющийся терминальным – внутренний узел. Путь к следующему уровню – ребро дерева (ветвь). Число “ветвей” определяет длину пути к определенному узлу.
Бинарное дерево – дерево, каждый узел которого соединен не более чем с 2мя поддеревьями.
Для построения идеально сбалансированного дерева минимальной высоты нужно располагать максимально возможное число узлов на всех уровнях, кроме самого нижнего. Алгоритмически это реализуется распределением узлов поровну справа или слева от каждого узла.
n
=1
n=2 n=3
n=4 n=5
Рекурсивная процедура, реализующая такую последовательность построения, должна состоять из следующих действий:
1. Выбрать один узел в качестве корня
2. Построить левое поддерево
nl=n div 2
3. Построить правое поддерево
nr=n-nl-1
Root:=nil;
New(p);
with p^ do
begin date:=x; left:=nil; rigth:=nil; end; Root:=p;
Если узел является терминальным, тогда поле ссылки равно null.
Основные операции над деревом:
1.Поиск элемента. 2.Удаление элемента. 3.Вставка элемента.
4.Упорядочить деревья по заданному признаку (не только сортировка).
5. Перемещение по дереву
Cбалансированное дерево. Сбалансированным считается дерево, если на каждом его уровне располагается максимально возможное число узлов.
1
.
Поиск
– это движение по дереву
Function Poisk(var t:node;r:integer):boolean;
var p :node;
flag :boolean;
begin
flag :=false;
p:=t;
while (p<> nil) and not flag do
if r = p^.date then flag:=true найден искомый элемент
else if r > p^.date then p: = p^.left
else p: = p^.right ; движение по узлам дерева
Poisk : =flag;
end;
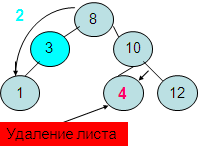
2. Удаление элементов созданного дерева.
2.1. Удаление листа – удаляется ссылка на лист из соответствующего поддерева
2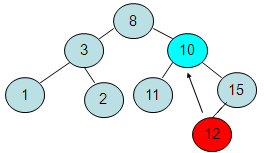
.2.
Удаление узла с одной ссылкой –
ссылку верхнего узла надо заменить на
удаляемую ссылку
2.3. Удаляемый узел содержит две ссылки – удаляемый узел замещается самым правым узлом левого поддерева или самым левым узлом правого поддерева
If r^. right =nil then begin
q^. date:=r^. date; - запоминаем значение
qk :=r; - сохраняем найденный узел
r :=r^. Left; Dispose(qk); end else {движение по правому поддереву}
Бинарное дерево поиска можно использовать для сортировки. Для этого берётся пустое дерево, к нему добавляют все элементы массива, а затем, используя алгоритм «Обход дерева», записывают элементы дерева в массив в возрастающем порядке.
class Tree {
public Tree left,right; // левое и правое поддеревья и ключ
public int key; // ключ
public Tree(int k) { key = k; }
/* insert (добавление нового поддерева (ключа)). сравнить ключ добавляемого поддерева (К) с ключом корневого узла (X).
Если K>=X, рекурсивно добавить новое дерево в правое поддерево. Если K<X, рекурсивно добавить новое дерево в левое поддерево. Если поддерева нет, то вставить на это место новое дерево */
public void insert( Tree aTree) {
if ( aTree.key < key ) if ( left != null ) left.insert( aTree );
else left = aTree; else
if ( right != null ) right.insert( aTree );
else right = aTree; }
/* traverse (обход)
Рекурсивно обойти левое поддерево. Применить функцию f (печать) к корневому узлу. Рекурсивно обойти правое поддерево. */
public void traverse(TreeVisitor visitor) { if ( left != null) left.traverse( visitor ); visitor.visit(this); if ( right != null ) right.traverse( visitor ); } } |
public void visit(Tree node);}
class KeyPrinter implements TreeVisitor {
public void visit(Tree node) { System.out.println( " " + node.key ); } }
public class TreeSort {
public static void main(String args[]) {
Tree myTree;
myTree = new Tree( 7 ); // создать дерево (с ключом)
myTree.insert( new Tree( 5 ) ); // присоединять поддеревья
myTree.insert( new Tree( 9 ) ); myTree.traverse(new KeyPrinter());}
void
preorder(CTreeNode* ctree, int k){ ctree->mark
= k;
if
(ctree->left!=null)
preorder(ctree->left,k+1);
if
(ctree->right != null) preorder(ctree->right,k+1);}