11010 Результат 01001

10011 Если разряды не совпадают, то результат =1

При хешировании ключей из символов или строк надо помнить, что

представление всех символов обеспечивается их цифровыми кодами

4.8.Решение задачи сортировки в массивах разных структур. Сравнение алгоритмов сортировки: методом вставки, включения, шейкер сортировки и быстрой сортировки. Примеры использования.

Сортировка данных – размещение всех значений некоторой структуры данных в соответствии с заданными значениями. Критерии:

1. Сортировка выполняется на том месте памяти, где записаны исходные данные.

2. Сортировка должна выполняться за наименьшее возможное время

3. Качеством сортировки является количество сравнений, количество перестановок.

Хорошие алгоритмы имеют количество сравнений C ~ log₁₀N, а плохие C ~ n².

Варианты сортировок:

1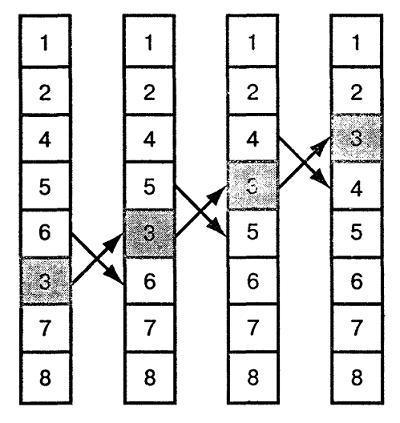 . Сортировка «методом пузырька»

2. Шейкер-сортировка

3. Быстрая сортировка (Хоора)

4. Сортировка вставкой

5. Сортировка включением

1. Bubble sort. При данном типе сортировки происходит итерационное перемещение большего / меньшего элемента вверх/вниз по числовой последовательности.

C~n*(n-1).

2. Shaker sort. Сортировка шейкером, чаще всего, применяется для упорядочивания очень больших массивов, которые возможно находятся на жёстком диске. Основная идея этого алгоритма заключается в том, чтобы в начале ycтpанить массовый беспорядок в массиве. Этот алгоритм за один проход цикла выбирает наибольший и наименьший элемент и помещает их соответственно в начало и конец списка (проходит в одну сторону – находит наибольший, в другую сторону – наименьший элемент). Затем операция повторяется и сортируются остальные элементы. Таким образом для сортировки всего массива понадобиться N\2 проходов цикла.

Анализ Шейкер – сортировки ББ Style

Задана последовательность неупорядоченных чисел. Окончание процесса сортировки обеспечивается неравенством left>right

3. Quick sort. Является существенно улучшенным вариантом алгоритма сортировки с помощью прямого обмена (его варианты известны как «Пузырьковая сортировка» и «Шейкерная сортировка»), известного, в том числе, своей низкой эффективностью. Принципиальное отличие состоит в том, что сначала берем элемент со средним значением для наилучшего результата, но можно взять с индексом N/2 – опорный элемент, и при проходе по циклу сравниваем все элементы относительно него и определяем их в левой и правой частях относительно этого опорного элемента. Далее тоже самое производим с оставшимися двумя половинами элементов.

Достоинства:

• Самый быстродействующий из всех существующих алгоритмов обменной сортировки — быстрее него только специализированные алгоритмы, использующие специфику сортируемых данных.

• Простая реализация.

• Хорошо сочетается с алгоритмами кэширования и подкачки памяти.

• Хорошо работает на «почти отсортированных» данных — если исходный массив уже близок к отсортированному, алгоритм не приводит к излишним перестановкам уже стоящих в правильном порядке элементов.

Недостатки:

• При классической реализации требует в худшем случае много дополнительной памяти. Правда, вероятность возникновения худшего случая ничтожна.

• Неустойчив — если нужна устойчивость, приходится расширять ключ.

Анализ быстрой сортировки ББ Style

Э тот алгоритм обеспечивает уменьшение числа обменов за счет обменов на больших расстояниях. Берем последовательность чисел из предыдущего примера. Выбираем некоторый средний элемент последовательности. Все меньшие его значения помещаются перед ним, а большие за ним

Окончание сортировки при left>right. Оценка времени выполнения быстрой сортировки в среднем ~ n * log (n).

Для других вариантов сортировки ~ O(n²).

Решение задачи на языке программирования по этому алгоритму обеспечивается созданием рекурсивной процедуры с новыми значениями левых и правых индексов сортируемой последовательности.

3. procedure InsertionSort( var a: array of integer; N: integer); var B: array [0..10000] of integer; i, j: integer; begin for i:=0 to N do begin j:=i; while ( j>1) and (B[ j-1]>A[i]) do begin B[ j]:=B[ j-1]; j:=j-1; end; B[ j]:=A[i]; end; for i:=0 to N do A[i]:=b[i]; end;

   Сортировка вставкой. Идея в том, чтобы создать новый массив, а затем последовательно вставлять в новый массив элементы из старого массива, чтобы созданный массив был всё время упорядоченным.

Если внимательно посмотреть на реализацию алгоритма, то сразу же заметим что для его выполнения необходимо больше, чем N*N проходов, поэтому в приложениях, где скорость выполнения кода критична, подобный алгоритм использовать не актуально.

3. Сортировка включением. Одним из наиболее простых и естественных методов внутренней сортировки является сортировка с простыми включениями. Идея алгоритма очень проста. Пусть имеется массив ключей a[1], a[2], ..., a[n]. Для каждого элемента массива, начиная со второго, производится сравнение с элементами с меньшим индексом (элемент a[i] последовательно сравнивается с элементами a[i-1], a[i-2] ...) и до тех пор, пока для очередного элемента a[j] выполняется соотношение a[j] > a[i], a[i] и a[j] меняются местами. Если удается встретить такой элемент a[j], что a[j] <= a[i], или если достигнута нижняя граница массива, производится переход к обработке элемента a[i+1] (пока не будет достигнута верхняя граница массива).

ББ Style Сортировка любых типов данных

1. Простые обменные сортировки: Обменом, Вставками, Выбором

2. Сортировка в разных направлениях (Шейкер)

3. Быстрая сортировка (Хоора)

4. Сортировка слиянием

5. Сортировка с убывающим приращением (Шелла)

6. Сортировка с помощью дерева

4.9.Понятие рекурсии. Использование рекурсии для записи решений. Древовидные структуры. Бинарное дерево. Правила обхода деревьев: инфиксная форма, префиксная форма, постфиксная форма. Примеры реализации обхода деревьев.

Объект называется рекурсивным, если он содержит сам себя или определен с помощью самого себя.

Рекурсия – обращение процедуры или функции самой к себе, прямо или косвенно. Когда функция обращается сама к себе, каждое последующее обращение сопровождается получением ею нового набора автоматических переменных, независимых от предыдущего набора.

Программы, написанные с помощью рекурсии, не обеспечивают ни экономии памяти, ни быстродействия; по сравнению с нерекурсивными программами они часто короче, а также намного легче для написания и понимания. Рекурсивные программы особенно удобны для обработки рекурсивно определяемых структур данных вроде деревьев.

Пример использования рекурсии– переворачивание строк, быстрая сортировка, предложенная Хоаром, подсчет частоты встречаемости для любых слов, реализуемой с использованием бинарных деревьев.

Рекурсии в математике:

1. а)0! б) n!=n*(n-1)! – эта формула позволяет вычисление любого нового значения на основе предыдущего его значения.

2. а) 1 – натуральное число

б) целое число, следующее за натуральным, есть натуральное число

3 . Кривая Гильберта

П оворотом можно получить кривые Гильберта любого порядка. Кривая следующего порядка получается соединением четырех кривых вдвое меньшего размера. Так строятся лабиринты. Кривые 1 и 2 порядков

Рекурсия выполняет медленнее, чем обычный цикл. т.к при каждом входе в подпрограмму её локальные переменные размещаются в программном стеке. Тем не менее, алгоритмы, реализуемые с помощью рекурсии, получаются значительно короче.

Древовидные структуры.

Дерево – это структура, содержащая узел T, с которым связано конечное число древовидных структур с базовым типом T, называемых поддеревьями. Узел, который не имеет потомков, называется терминальным или листом.

Узел, не являющийся терминальным, называется внутренним узлом. Линии связей между узлами называются ветвями дерева. Число ветвей, которые надо пройти, чтобы продвинуться от корня A к узлу B, называется длиной пути. Каждый из узлов в таком представлении дерева находится на определенном уровне. Корень дерева имеет уровень, равный 1. Максимальный уровень какого-либо узла называется его глубиной или высотой.

Деревья, имеющие степень ветвления больше двух, называются сильно ветвящимися деревьями. Далее рассматриваются бинарные деревья.

Бинарное дерево – дерево, каждый узел которого соединен не более чем с 2мя поддеревьями. Информационное поле узла дерева может быть любого типа, определенного ранее, а связи между узлами – это ссылки на узлы того же типа.

Type node=^nnode;

nnode = record

date: <тип данных>;

left, right : node;

end;

var root, p, q : node;

Если узел является терминальным, тогда поле ссылки равно null.

Основные операции над деревом:

1.Создание дерева

2.Поиск элемента - перемещение по дереву

3.Удаление элемента.

4.Вставка элемента.

5.Упорядочить деревья по заданному признаку (не только сортировка).

Cбалансированное дерево. Сбалансированным считается дерево, если на каждом его уровне располагается максимально возможное число узлов поровну слева и справа.

Для построения идеально сбалансированного дерева минимальной высоты нужно располагать максимально возможное число узлов на всех уровнях, кроме самого нижнего. Алгоритмически это реализуется распределением узлов поровну справа или слева от каждого узла:

1. Выбрать один узел в качестве корня

2. Построить левое поддерево 

nl=n div 2

3. Построить правое поддерево 

nr=n-nl-1

Root:=nil;

New(p);

with p^ do

begin date:=x; left:=nil; rigth:=nil; end; Root:=p;

Обход дерева - это некоторая последовательность посещения всех его вершин.

Инфиксная форма. Это обычный вариант прочтения арифметических выражений, когда знак операции помещается между операндами. Порядок вычисления выражения слева направо в соответствии с приоритетом операций. Скобки изменяют порядок вычислений. SIN (X) *C – D+E/F/(G+H)

Префиксная форма. Вариант прочтения арифметических выражений, когда знак операции помещается перед операндами. + - * SIN(X)CD/EF/+GH

Постфиксная форма (Обратная польская запись). Вариант прочтения арифметических выражений, когда знак операции помещается после операндов. SIN(X) C*D-EFGH+//+

Обратный обход/постфиксный обход: Начинаем обход дерева с самого левого листа. Поднимаемся к знаку. Далее спускаемся к листу. Прочитанное выражение будет обычной формой записи выражений.

P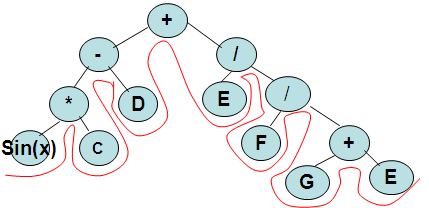 rocedure Infixprint(var p:nn);

begin

if p<> nil then

begin

Infixprint(p^.left);

write(p^.date);

Infixprint(p^.right);

end; end;

Постфиксный обход: читаем дерево снизу вверх, как показано на рис.

P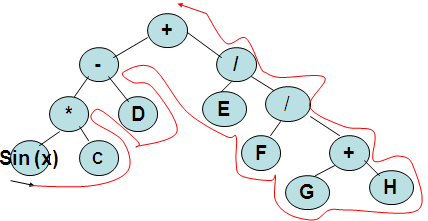 rocedure Postprint(var p:nn);

begin

if p<> nil then

begin

Postprint(p^.left);

Postprint(p^.right);

write(p^.date);

end;end;

Прямой обход/Префиксный обход: результатом прямого обхода дерева будет префиксный вариант записи этого выражения.

1. Начать с корня дерева.

2. Пометить текущую вершину.

3. Совершить прямой обход левого поддерева.

4. Совершить прямой обход правого поддерева.

P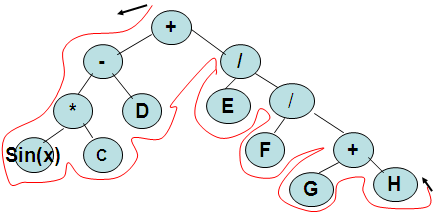 rocedure Prefprint (var p:nn);

begin

if p<> nil then

begin

write(p^.date);

Prefprint(p^.left);

Prefprint(p^.right);

end;end;