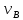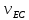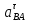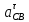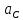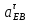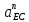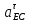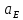Артоболевский. Теория механизмов и машин. Задачи / Артоболевский. Теория механизмов и машин. Задача 111

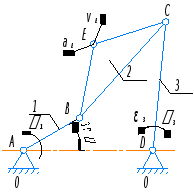
111. _{Найти абсолютные скорость и ускорение точки} E и угловые скорость и ускорение звена CD (звена 3) четырехзвенного четырехшарнирного механизма. Дано: l_AB=30 мм, l_BC=l_CD=l_AD=60 мм, l_BE=l_CE=35 мм, φ₁=30°, угловая скорость кривошипа AB (звена 1) постоянна и равна ω₁=20 с^-1.

Для построения плана положений механизма необходимо:

проставить точки опоры A и D;

из точки A построить отрезок AB длиной l_AB под углом φ₁;

из точек B и D построить отрезки BC и CD длинами l_BC и l_CD до совпадения (точка C) соответственно;

из точек B и C построить отрезки BE и CE длинами l_BE и l_CE до совпадения (точка E) соответственно.

Для построения плана скоростей механизма необходимо:

проставить полюс скоростей;

отложить от полюса вектор скорости точки B (перпендикулярно AB в направлении движения кривошипа);

отложить от конца вектора скорости точки B (перпендикулярно BC) и от полюса (перпендикулярно CD) до совпадения векторы скоростей точки C относительно точки B и точки C соответственно;

отложить от конца вектора скорости точки B (перпендикулярно BE) и от конца вектора скорости точки C (перпендикулярно CE) до совпадения векторы скоростей точки E относительно точек B и C соответственно;

отложить от полюса в точку совпадения векторов скоростей точки E относительно точек B и C вектор скорости точки E.

;

;

.

.

.

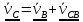м/с	0,6	0,827	0,317	0,482	0,482	0,463

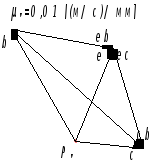
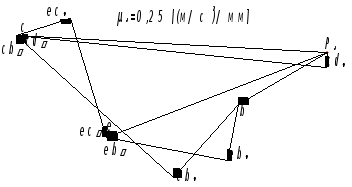
Для построения плана ускорений механизма необходимо:

проставить полюс ускорений;

отложить от полюса вектор ускорения точки B (параллельно AB в направлении от точки B к точке A);

отложить от конца вектора ускорения точки B (параллельно BC в направлении от точки C к точке B) и от полюса (параллельно CD в направлении от точки C к точке D) векторы нормальных ускорений точки C относительно точек B и D соответственно;

отложить от конца вектора нормального ускорения точки C относительно точки B (перпендикулярно BC) и от конца вектора нормального ускорения точки C относительно точки D (перпендикулярно CD) до совпадения векторы тангенциальных ускорений точки C относительно точек B и D соответственно;

отложить от полюса в точку совпадения векторов тангенциальных ускорений точки C относительно точек B и D вектор ускорения точки C;

отложить от конца вектора ускорения точки B (параллельно BE в направлении от точки E к точке B) и от конца вектора ускорения точки C (параллельно CE в направлении от точки E к точке C) векторы нормальных ускорений точки E относительно точек B и C соответственно;

отложить от конца вектора нормального ускорения точки E относительно точки B (перпендикулярно BE) и от конца вектора нормального ускорения точки E относительно точки C (перпендикулярно CE) до совпадения векторы тангенциальных ускорений точки E относительно точек B и C соответственно;

отложить от полюса в точку совпадения векторов тангенциальных ускорений точки E относительно точек B и C вектор ускорения точки E.

;

;

;

;

;

;

;

;

;

;

.

.

.

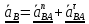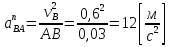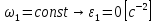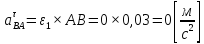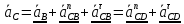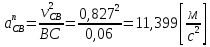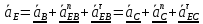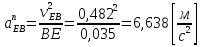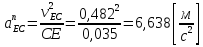м/с2	12	0	12	11,4	24,7	1,7	36,4	36,4	6,6	14,4	6,6	14,4	27,6