69. Криволинейные интегралы второго рода

Определение

Предположим, что кривая C задана векторной функцией , где переменная s − длина дуги кривой. Тогда производная векторной функции

представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1).

В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осей Ox, Oy и Oz, соответственно.

Рис.1 Рис.2

Введем векторную функцию , определенную на кривой C, так, чтобы для скалярной функции

существовал криволинейный интеграл . Такой интеграл называется криволинейным интегралом второго рода от векторной функции вдоль кривой C и обозначается как

Таким образом, по определению,

где − единичный вектор касательной к кривой C.

Последнюю формулу можно переписать также в векторной форме:

где .

Если кривая C лежит в плоскости Oxy, то полагая R = 0, получаем

Свойства криволинейного интеграла второго рода

Криволинейный интеграл II рода обладает следующими свойствами:

1. Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −C кривую противоположного направления - от B к A. Тогда

2. Если C − объединение кривых C1 и C2 (рисунок 2 выше), то

3. Если кривая C задана параметрически в виде , то

4. Если кривая C лежит в плоскости Oxy и задана уравнением (предполагается, что R =0 и t = x), то последняя формула записывается в виде

Пример 1

Вычислить интеграл , где кривая C задана параметрически в виде .

Решение. Используя формулу

находим ответ:

71.

72.Вычисление поверхностного интеграла.

Если существует конечный предел

не зависящий от способа разбиения поверхности S на "элементарные" участки ΔSi и от выбора точек Mi  ΔSi(i=1,....n), то он называется поверхностным интегралом первого рода от функции f(x,y,z) по поверхности S и обозначается

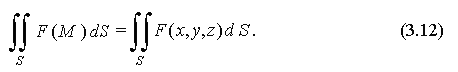
К использованию этих условий, равно как и условий, получающихся из них перестановкой переменных x, y, z сводится большинство практически встречающихся случаев по плоской области τ. Переходя к пределу, получаем:

73. формула Стокса, формула преобразования криволинейного интеграла по замкнутому контуру L в поверхностный интеграл по поверхности S, ограниченной контуром L. Стокса формула имеет вид:    ,    причём направление обхода контура L должно быть согласовано с ориентацией поверхности S. В векторной форме Стокса формула приобретает вид: ,   где а = Pi + Qj + Rk, dr — элемент контура L, ds — элемент поверхности S, n — единичный вектор внешней нормали к этой поверхности.

74. Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля пообъёму, ограниченному этой поверхностью:

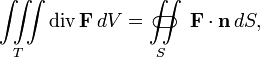
то есть интеграл от дивергенции векторного поля  , распространённый по некоторому объёму  , равен потоку вектора через поверхность  , ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.

В работе Остроградского формула записана в следующем виде:

где   и   — дифференциалы объёма и поверхности соответственно. В современной записи   — элемент объёма,   — элемент поверхности.   — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.

23.

Метод замены переменной

Рассмотрим неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой.  Важно иметь ввиду, что дифференциал dx должен быть заменен на дифференциал новой переменной du.  Для определенного интеграла, кроме этого, необходимо также изменить пределы интегрирования.