1.3. Абстрактные графы

Ребра	Вершины, соответствую­щие ребрам
е\	Из. v6
е2	Vi, Уз
е%	Vi, v3
е4	Vi
ев	Vi, V4
е6	»2, Vt
	Vi

Хотя многие графы, представляющие реальные объ­екты (после их идеализации), являются геометрически­ми графами, сточки зрения теории графов их единствен­ная структурная особенность состоит в том, что с каж­дым геометрическим ребром связаны две (возможно сов­падающие) геометрические вершины. Теория графов пост­роена с учетом именно этой особенности и не учитывает реальной природы вершин и ребер. Таким образом, нуме­рация ребер и вершин, задаваемая нижеследующей таб­лицей, содержит всю информа­цию, необходимую для описания геометрического графа рис. 1.1.

Для облегчения общего опре­деления графа введем понятие не­упорядоченного произведения множества само на себя. Напом­ним, что упорядоченным или декартовым (прямым) произведе­нием множества S само на себя (которое обозначается SX.S) на­зывается множество всех упоря­доченных пар (s, (), где,j^S и feS. Здесь (s, t) и (/, s) рассматриваются как различные элементы, исключая случай s — t. Аналогично, символом (s&t) будем обозна­чать неупорядоченную пару элементов множества S, а множество всех различных неупорядоченных пар будет обозначаться как S&S и называться неупорядоченным произведением множества S само на себя. В данном случае (s&t) и (t&s) эквивалентны и так Тке, как при декартовом произведении, допускается совпадение эле­ментов пары, т. е. s=t. Заметим, что если s имеет & эле­ментов, то SXS состоит из k² упорядоченных пар, a S&S — из k(k-{-l)/2 различных неупорядоченных пар.

Абстрактный граф или просто граф можно определить теперь следующим образом.

Граф есть совокупность непустого множества V, изо­лированного от него множества Е (возможно пустого) и отображения Ф множества Е на V&V. Элементы мно­жеств V и Е называются вершинами и ребрами графа соответственно, а Ф называется отображением инциден­ту ии графа.

Если ее/Г—ребро, а веУ иэдеУ — вершины такие, что Ф (е) =v&w, говорят, что ребро е инцидентно каж­дое из вершин и и и обратно. Все остальные вершины рассматриваются как не инцидентные ребру е. Вершины, ■ндидентные ребру, называются его граничными точками. Иногда говорят, что они соединяются ребром е.

Хотя отношение инцидентности является фундамен­тальным в понятии графа, отображение Ф часто можно ве задавать в явном виде. В таких случаях, если v и w — граничные точки ребра е, то это обозначается е~ (v&w) а читается «е соединяет вершины v и w».

Будем обозначать граф через G или (V, Е, Ф) или (V, Е). Последнее обозначение используем, когда отно­шение инцидентности определяется не явно. Заметим, что множество Е (но не V) может быть пустым. Говорят, что граф вырожденный тогда и только тогда, когда он не имеет ребер. Хотя графы, не имеющие ребер, сами по себе не интересны, их рассмотрение иногда оказывается полезным, например, при работе с процедурами разборки графа, основанными на последовательном удалении ребер.

Если V и Е — конечные множества (пустое множест­во тоже рассматривается как конечное), то G называет­ся конечным графом. В противном случае говорят, что вдаф не является конечным.

Введение понятия абстрактного графа позволяет не «ими избавиться от случайных геометрических характе­ристик, сохранив наиболее существенные комбинаторные свойства графа. Оно расширяет возможности приложения •теории, так как многие реальные структуры имеют ком­бинаторные свойства, которые полезно рассматривать tax граф. Например, в виде графа можно задать соот­ношение между отдельными работами, которые состав­ляют сложные проекты. В этом случае ребра (после то-' to как задана их ориентация или направление, см. гла­ву 2) представляют отдельные работы, а отношения

существенные отличия с точки зрения топологии, с точки зрения теории графов они эквивалентны.

Рис. 1.2.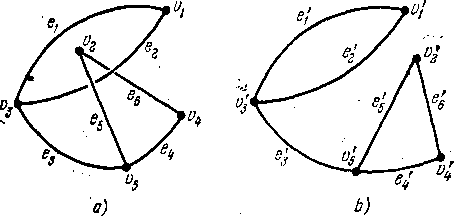

Рис. 1.3.

Нл рис. 1.3 показан неплоский граф, т. е. граф, не имею шин геометрической реализации в пространстве е². Граф иллюстрирует одну из двух фундаментальных кон­фигураций, которые характеризуют асе иеплоские конечные графы.

Этот результат, следующий из важ- иой теоремы, принадлежащей Ку- рвтовскому ¹), устанавливается в 4, где исследуются особенно- плоских графов. Если в про- схравстве е² только ограниченный агг конечных графов имеет гео- ■ырическую реализацию, то для 1анства е³ справедливо следу- утверждение.

■а 1.1. Любой конечный граф G имеет геомет-. реализацию в е³.

Л*«аз а те л ь с т в о. Обозначим через L произволь- ■рямую в е³. Поставим в соответствие каждой вер- е ref определенную точку v' на L (различным вер- ал с будут соответствовать различные v'), а каж. неупорядоченной паре (и&оОеУ&У — определен- волуплоскость H_v- границей которой является L.

[ГЛ. £

У.

Для каждого ребра е из G такого, что е~ (v&w), постро­им в полуплоскости Я... простую кривую е\ соединяю­щую v' и w' и не имеющую других общих точек с L или с другими кривыми в Я.,». (Очевидно, что это возмож­но.) Полученная структура является геометрической ре­ализацией графа G в е³.

Хотя справедливость теоремы 1.1 почти очевидна, мы указали этот способ построения геометрической реали­зации главным образом потому, что его можно непос­редственно обобщить для доказательства следующей, менее очевидной теоремы, которая определяет наличие геометрической реализации в самом общем виде.

Теорема 1.2. Граф G=(V, Е) имеет геометрическую реализацию в е³ тогда и только тогда, когда элементам V и Е можно поставить во взаимно однозначное соответ- ветствие некоторое подмножество множества действи­тельных чисел.

Для читателя, знакомого с понятием кардинального числа, сказанное означает, что G имеет реализации в е³ тогда и только тогда, когда кардинальные числа мно­жеств V и Е совпадают с кардинальными числами кон­тинуума.

Далее мы почти всегда будем иметь дело с конечными графами и исключим из рассмотрения графы, которые не удовлетворяют условиям теоремы 1.2. Более того, все изучаемые структурные свойства сохраняются за счет изоморфизма, так как они в конечном счете основывают­ся на понятии инцидентности. Из сказанного следует, что далее без потери общности можно все рассуждения проводить полностью в терминах геометрических реа­лизаций в е³. В частности, все графы, которые будут иллюстрировать излагаемый материал, являются геомет­рическими графами.

Идея доказательства теоремы 1.2 состоит в следую­щем. Точки пространства е" можно взаимнооднозначно отобразить на множество действительных чисел. Очевид­но, что граф G(V, Е) не имеет реализации в е³ (и даже в е” для любого положительного целого п), если нельзя установить взаимно однозначного соответствия между некоторым множеством его вершин или ребер и подмно­жеством точек в е³. С другой стороны, если такое соот­ветствие существует, то можно (в терминологии доказа-

тельства теоремы 1.1) выбрать различные точки v' на L для каждой вершины и различные полуплоскости //„, „ для каждой неупорядоченной пары вершин. Как только это сделано, в плоскости Я„ _w можно построить кривые согласно схеме, показанной на рис. 1.4. Каждая точка на

Рис. 1.4.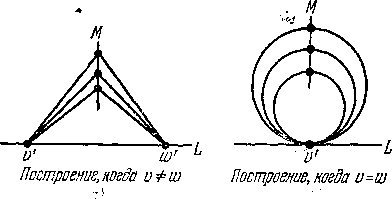

отрезке М определяет простую кривую (ломаную линию или круг), которая не совпадает с другими такими же кривыми, за исключением точек v' и w'.