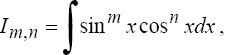3. Интегрирование тригонометрических функций.

1°. Интегралы вида

находятся с помощью тригонометрических формул

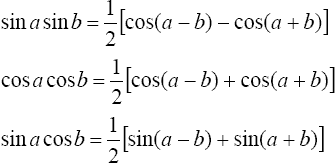
2°. Интегралы вида

4. 

где m и n - четные числа находятся с помощью формул понижения степени

Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

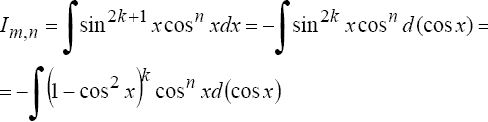
Вопрос 16.

Понятие определенного интеграла. Предел интегральной суммы.

1. Понятие определенного интеграла.

Определенный интеграл (Римана) позволяет распространить формулу площади прямоугольника на площадь более или менее произвольной плоской геометрической фигуры. В основе понятия определенного интеграла лежит так называемая интегральная сумма, определяемая следующим образом. Пусть задана функция 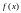, определенная на отрезке 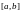. Разобъем отрезок произвольным образом на частей 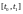, 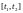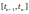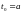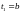, ( , ). В частности, можно разбить на равных частей, тогда длина каждого отрезка разбиения будет равна 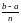. В общем случае, пусть

.

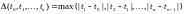Возьмем, опять же произвольным образом, внутри каждого из отрезков 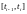по точке 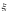. Интегральной суммой функции на по разбиению 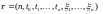называется число

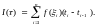
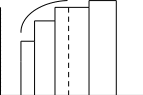
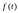
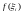
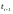
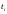
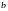
Если 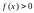, то интегральная сумма есть площадь фигуры, состоящей из прямоугольников со сторонами и , 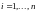. Интуитивно ясно, что, чем меньше максимальная длина отрезков разбиения 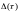, тем точнее эта фигура из прямоугольников приближает криволинейную трапецию с основаниями , 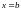и “боковыми сторонами” 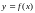, 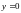. Интеграл от функции по отрезку есть предел 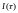по всевозможным разбиениям , когда .

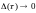Предел понимается здесь в обычном смысле: число 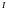называется определенным интегралом от по (обозначается как 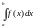), если для произвольного 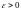найдется такое 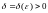, что, как только разбиение отрезка удовлетворяет условию 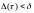, интегральная сумма , отвечающая этому разбиению, будет отличаться от не больше, чем на : .

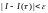2. Предел интегральной суммы

Пусть функция у=ƒ(х) определена на отрезке [а; b], а < b. Выполним следующие действия.

1. С помощью точек х₀=а, x_1, х_{2, ...,} х_n = В (х₀ <x₁ < ...< х_n) разобьем отрезок [а, b] на n частичных отрезков [х₀;х₁], [x₁; х₂],..., [х_n-1,х_n] (см. рис. 167).

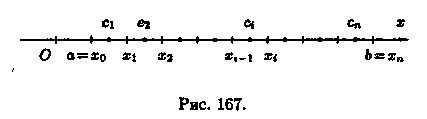
2. В каждом частичном отрезке [x_i-1;x_i], i = 1,2,...,n выберем произвольную точку с_i є [x_i-1; x_i] и вычислим значение функции в ней, т. е. величину ƒ(с_i).

3. Умножим найденное значение функции ƒ (с_i) на длину ∆x_i=x_i-x_i-1 соответствующего частичного отрезка: ƒ (с_i) • ∆х_i.

4. Составим сумму S_n всех таких произведений:

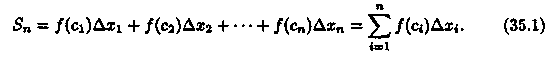
Сумма вида (35.1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b]. Обозначим через λ длину наибольшего частичного отрезка: λ = max ∆x_i(i = 1,2,..., n).

5. Найдем предел интегральной суммы (35.1), когда n → ∞ так, что λ→0.

Если при этом интегральная сумма S_n имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = ƒ(х) на отрезке [а; b] и обозначается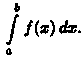 Таким образом,

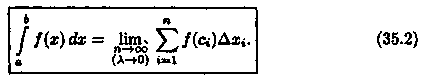
Числа а и b называются соответственна нижним и верхним пределами интегрирования, ƒ(х) — подынтегральной функцией, ƒ(х) dx — подынтегральным выражением, х — переменной интегрирования, отрезок [а; b] — областью (отрезком) интегрирования.