Вопрос 14.

Понятие первообразной функции и неопределенного интеграла. Основные свойства неопределенного интеграла. Таблица основных неопределенных интегралов. Интегрирование заменой переменной и по частям.

1. Понятие первообразной функции и неопределенного интеграла.

Ф-ия F(x) называется первообразной для f(x) на промежутке M_, если F’(x)=f(x) для всех х M.

Неопределенный интеграл от функции f(x) совокупность всех первообразных ф-ии f(x).

= F(x)+ C

2. Основные свойства неопределенного интеграла:

1. = F(x)+ C

2. 

3. = c

3. Таблица основных интегралов

4. Интегрирование заменой переменной и по частям.

Замена:

Рассмотрим неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением

где x = g (u) - подстановка. Соответственно, обратная функция u = g ⁻¹(x) описывает зависимость новой переменной от старой. Важно иметь ввиду, что дифференциал dx должен быть заменен на дифференциал новой переменной du. 

Пример:

По частям:

Пример:

Вопрос 15.(посмотри в никишкине)

Интегрирование рациональных выражений. Интегрирование некоторых иррациональных. Интегрирование тригонометрических функций.

1. Интегрирование рациональных выражений.

Рациональной дробью называется выражение вида  , где  , –многочлены степеней n и m соответственно.

Если  , рациональная дробь называется правильной, в противном случае  –неправильной.

Если дробь неправильная, из нее можно выделить целую часть, разделив числитель на знаменатель.

Способ интегрирования рациональной ф-ии заключается в представлении ее в виде сумы простейших дробей с помощью метода неопределенных коэффициентов.

Простейшие дроби:

Знаменатель правильной дроби разлагается на множители вида (x-a)m и (x2+px+q)n, D<0, правильная дробь разлагается в сумму элементарных дробей:

= + +…+ + + +… +

2. Интегрирование некоторых иррациональных

Функции, содержащие иррациональности, интегрируются в том случае, когда интеграл от них сводится к интегралу от рациональной дроби с помощью какойлибо замены переменной. Приведем несколько примеров интегрируемых иррациональных функций.

) Интегралы вида

где  рациональная функция, а , ,  натуральные числа. Метод интегрирования  замена , где  наименьшее общее кратное чисел , , .

) Интегралы вида сводятся к табличным при помощи замены .

) Интегралы , где , и  рациональные числа. Интегралы такого вида сводятся к элементарным только при следующих соотношениях параметров , и .

Если целое, то следует использовать замену , где  наименьшее общее кратное знаменателей дробей , .

Пусть теперь  наименьшее общее кратное знаменателей дробей , . Если  целое, то интеграл сводится к интегралу от рациональной функции с помощью замены .

Если целое, то интегрирование осуществляется при помощи замены .

) Подстановки Эйлера. Они применяются к интегралам вида , где рациональная функция. Имеется три вида подстановок Эйлера.

;

;

,

где , корни многочлена .

Тригонометрические замены. Для интегралов используется замена . Для интегралов используется замена . Для интегралов используется замена 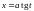. В каждом из трех случаев получается интеграл от рациональной функции, зависящей от и .