
- •Вопрос 1.
- •Вопрос 2.
- •Геометрические св-ва:
- •Алгебраические св-ва:
- •Выражение сп в дпк:
- •Вопрос 3.
- •Геометрические св-ва вп.
- •Вопрос 4.
- •Вопрос 5.
- •Вопрос 6
- •Вопрос 7.
- •Параметрические и канонические уравнения прямой в пространстве.
- •Прямая как линия пересечения двух плоскостей (общие уравнения прямой).
- •Угол между двумя прямыми в пространстве.
- •Условие параллельности и перпендикулярности прямых в пространстве.
- •Вопрос 8.
- •Точка пересечения прямой и плоскости.
- •Вопрос 9.
- •Предел функции.
- •Арифметические операции над функциями.
- •Доказательство?!?!
- •Первый и второй замечательный пределы.
- •Вопрос 10.
- •Доказательство?! (доказывается с помощью пределов:
- •Вопрос 11.
- •Геометрический смысл:
- •Вопрос 12.
- •Вопрос 13.
- •Вопрос 14.
- •Понятие первообразной функции и неопределенного интеграла.
- •Основные свойства неопределенного интеграла:
- •Интегрирование заменой переменной и по частям.
- •Вопрос 15.(посмотри в никишкине)
- •Интегрирование рациональных выражений.
- •Интегрирование некоторых иррациональных
- •Интегрирование тригонометрических функций.
- •Вопрос 16.
- •Понятие определенного интеграла.
- •Предел интегральной суммы
- •Вопрос 17.
- •Вопрос 18.
- •Вопрос 19.
- •Несобственные интегралы от неограниченных функций
- •Вопрос 20.
Вопрос 2.
Скалярное произведение векторов, его свойства, геометрический смысл и выражение в декартовых прямоугольных координатах
Определение. СП двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
(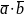 )=
|
|
)=
|
|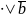 |
|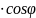 (1)
(1)
Или:
(
)=
|
|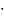 ПР
ПР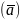 или (
)=
|
|
ПР
или (
)=
|
|
ПР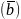
Геометрические св-ва:
Теорема1. Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Доказательство:
1) Необходимость. Пусть векторы
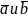 ортогональны,
ортогональны,
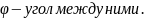 Тогда cos
Тогда cos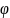 = 0 и, в силу формулы (
)=
0
= 0 и, в силу формулы (
)=
0
2)Достаточность. Пусть ( )= 0. Докажем, что векторы ортогональны. Если хотя бы один из векторов является нулевым, то он ортогонален любому вектору.
Если векторы не нулевые, то | |>0, | |>0, поэтому из равенства ( )= | | | =0 вытекает, что cos =0, т.е. векторы ортогональны, ч.т.д.
Теорема 2. Два ненулевых вектора составляют острый(тупой) угол тогда и только тогда, когда их СП положительно(отрицательно).
Алгебраические св-ва:
( )= (
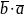 )
следует из ф-лы (1)
)
следует из ф-лы (1)((k )
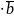 )=k(
)
следует из ((k
)
)=
|
|
ПР
(k
)=k|
|
ПР
=
k(
)
)=k(
)
следует из ((k
)
)=
|
|
ПР
(k
)=k|
|
ПР
=
k(
)(
 )
)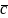 = (
= (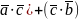
(
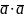 )
> 0 , если вектор
ненулевой вектор, и (
)
= 0, если
- нулевой вектор. Следует из |
)
> 0 , если вектор
ненулевой вектор, и (
)
= 0, если
- нулевой вектор. Следует из |
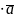 |=|
|2
|=|
|2
Выражение сп в дпк:
Если векторы заданы своими координатами {a1,a2,a3} и {b1, b2 ,b3}, то
= a1b1+a2b2+a3b3. Тогда
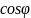 =
=
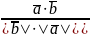 =
=
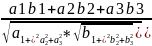
Доказательство?!
Векторы
единичной длины, направленные вдоль
осей координат обозначаются как
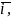
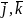 – они образуют базис в пространстве.
– они образуют базис в пространстве.
{a1,a2,a3}
a1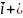 a2
a2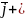 a3
a3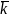 - разложили вектор по базису
- разложили вектор по базису
Вопрос 3.
Векторное произведение векторов, его свойства, геометрический смысл и выражение в декартовых прямоугольных координатах
Определение. ВП [
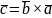 ]
называется вектор
такой, что:
]
называется вектор
такой, что:
а)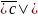 равна
S
параллелограмма, построенного на
векторах
равна
S
параллелограмма, построенного на
векторах
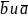 ,
т.е.
=
,
т.е.
=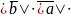 sin
sin
б) вектор ортогонален к каждому из векторов ,
в) направлен таким образом, что кратчайший поворот от к осуществляется против часовой стрелки, если его рассматривать из конца
Геометрические св-ва вп.
Теорема1. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их ВП.
Доказательство.
1)Необходимость вытекает из определения ВП.
2)
Достаточность. Пусть [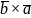 ]=0.
Докажем, что векторы
коллинеарны. Если хотя бы один из векторов
является нулевым, то он коллинеарен
любому вектору.
]=0.
Докажем, что векторы
коллинеарны. Если хотя бы один из векторов
является нулевым, то он коллинеарен
любому вектору.
Если же оба вектора ненулевые, то | |>0, | |>0 и поэтому из равенства
[
]=
sin
= 0 следует , что sin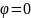 ,
,
т.е. векторы
коллинеарны, ч.т.д.
,
,
т.е. векторы
коллинеарны, ч.т.д.
Алгебраические св-ва ВП:
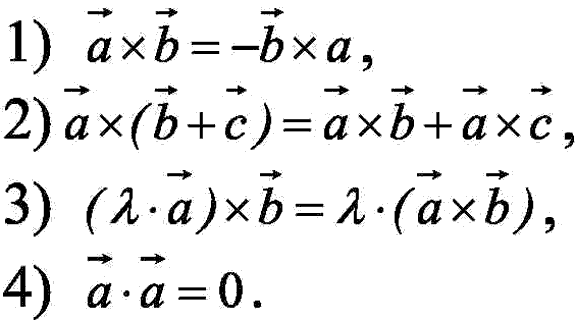
Выражение ВП в ДКП.
Если векторы и заданы своими координатами
{a1 a2 a3} и { b1 b2 b3}, то их ВП имеет вид:
[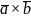 ]
=
]
=
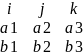 =
=
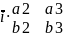 –
–
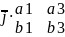 +
+
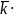
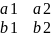
Доказательство?!
Вопрос 4.
Смешанное произведение векторов, его свойства, геометрический смысл и выражение в декартовых прямоугольных координатах.
Определение.
Смешанным
произведением 3ех векторов называется
выражение вида:
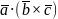 .
.
Геометрический смысл:
модуль
смешанного
произведения равен объему параллелепипеда,
построенного на приведенных к общему
началу векторах
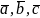 .
.
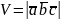
Объем пирамиды , построенной на векторах вычисляется как:
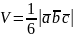
Выражение в ДПК
Если три вектора заданны своими координатами
{a1 a2 a3} , { b1 b2 b3} и {c1, c2 ,c3}, то
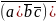 =
=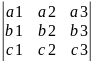
Доказательство?!
