
Вычисление площади фигуры, ограниченной кривой, заданной в параметрическом виде.
Пусть x=x(t), y=y(t),
где ![]() -
параметрические уравнения кусочно-гладкой
кривой. Если данные уравнения определяют
некоторую функцию y=f(x)
на отрезке [a,b]
(без ограничения общности будем считать,
что
-
параметрические уравнения кусочно-гладкой
кривой. Если данные уравнения определяют
некоторую функцию y=f(x)
на отрезке [a,b]
(без ограничения общности будем считать,
что ![]() на
отрезке [a,b]),
то площадь криволинейной трапеции,
ограниченной осью OX,
кривой y=f(x)
и прямыми x=a и x=b,
может быть найдена по формуле
на
отрезке [a,b]),
то площадь криволинейной трапеции,
ограниченной осью OX,
кривой y=f(x)
и прямыми x=a и x=b,
может быть найдена по формуле 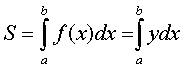 .
.
Вводя замену переменной y=y(t), x=x(t), dx= x’(t)dt, получим формулу для вычисления площади фигуры при параметрическом задании границы:
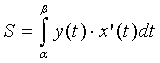 .
.
Аналогично может быть получена формула
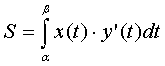 .
.
Таким образом, вычисление площади фигуры, ограниченной кривой в параметрической форме, может быть рассмотрено как замена переменной при вычислении площади в декартовых координатах.
Если x=x(t), y=y(t), ![]() -
параметрические уравнения кусочно-гладкой
замкнутой кривой, пробегаемой в
положительном направлении (то есть
таким образом, что фигура, ограниченная
заданным контуром остается слева), то
площадь S этой
фигуры равна:
-
параметрические уравнения кусочно-гладкой
замкнутой кривой, пробегаемой в
положительном направлении (то есть
таким образом, что фигура, ограниченная
заданным контуром остается слева), то
площадь S этой
фигуры равна:
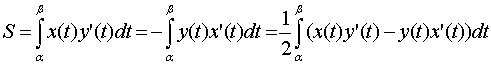 ,
,
где ![]() -
значения параметра, соответствующие
началу и концу обхода контура фигуры в
положительном направлении.
-
значения параметра, соответствующие
началу и концу обхода контура фигуры в
положительном направлении.
Пример
1. Найти площадь фигуры, ограниченной
кривой, заданной параметрически: ![]() .
.
Решение.
Выясним, какую фигуру ограничивает
заданная кривая. Функции x=x(t)
и y=y(t)
определены, непрерывны и дифференцируемы
при любом действительном значении
параметра ![]() .
Если
.
Если ![]() ,
то
,
то ![]() ,
а если
,
а если ![]() ,
то
,
то ![]() .
.
Наибольшее значение x принимает при x’(t)=0, 2-2t=0; t=1, x(1)=1; y(1)=1. Если x=0, то t=2 или t=0. При этих же значениях параметра y=0. Таким образом, точка с координатами (0;0) является точкой самопересечения. Следовательно, искомая площадь ограничена петлей кривой, расположенной в первом квадранте, и соответствует изменению параметра от t=0 до t=2 при положительном направлении обхода (рисунок 7).
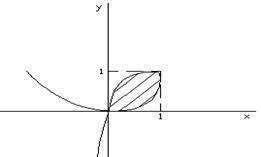
Рисунок 7.
Площадь искомой фигуры можно вычислить по формуле
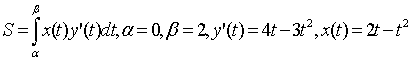 ,
,
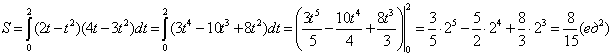 .
.
Поскольку некоторые кривые могут быть заданы простыми параметрическими уравнениями, то вычисление площади фигуры, ограниченной замкнутой кривой, в декартовых координатах зачастую удобнее проводить, перейдя к параметрической форме записи.
Пример
2. Вычислить площадь фигуры ограниченной
эллипсом ![]() .
.
Решение.
Запишем уравнение эллипса в параметрической
форме: x=a×cost, y=b×sint, ![]() .
Возрастание параметра от 0 до
2p соответствует
положительному направлению обхода.
Наиболее простой вид подынтегральное
выражение примет, если воспользоваться
формулой
.
Возрастание параметра от 0 до
2p соответствует
положительному направлению обхода.
Наиболее простой вид подынтегральное
выражение примет, если воспользоваться
формулой
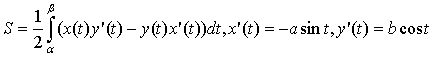 ;
;
![]() ;
;
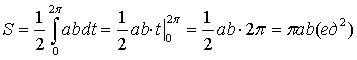 .
.
Вычисление длины дуги кривой.
Пусть
в декартовой системе координат на
плоскости дана кривая, являющаяся
графиком непрерывной дифференцируемой
функции y=f(x)
с непрерывной производной на отрезке
[a,b].
Разобьем отрезок [a,b]
произвольным образом на n частей
точками ![]() .
Найдем значения функции f(x)
в точках разбиения. Тогда дуга кривой f(x)
на [a,b]
разобьется на n частей
точками
.
Найдем значения функции f(x)
в точках разбиения. Тогда дуга кривой f(x)
на [a,b]
разобьется на n частей
точками
![]() .
Проведем хорды
.
Проведем хорды ![]() и
обозначим их длины
и
обозначим их длины ![]() соответственно.
Полученная ломаная
соответственно.
Полученная ломаная![]() имеет
длину
имеет
длину 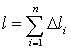 .
.
Определение. Длиной дуги кривой y=f(x) на отрезке [a,b] называется предел, к которому стремится длина вписанной ломаной при стремлении к нулю длины ее наибольшего звена (или, что то же самое, при неограниченном увеличении числа точек деления)
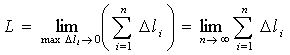 .
.
Длина
отдельного звена ломаной может быть
найдена как длина отрезка ![]() :
:
![]() .
.
Поскольку
функция f(x)
непрерывна и дифференцируема на всем
промежутке [a,b],
то, по теореме Лагранжа о дифференцируемых
функциях, найдется такая точка ![]() на
отрезке
на
отрезке![]() ,
что
,
что
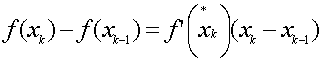 .
.
Если
обозначить ![]() ,
то формулу для
,
то формулу для ![]() можно
переписать в виде
можно
переписать в виде
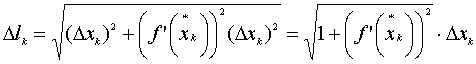
Таким образом, длина дуги y=f(x) на отрезке [a,b] определяется формулой
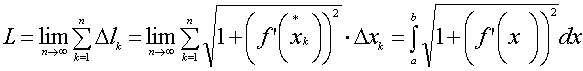
в
силу непрерывности f’(x)
и определения интегральной суммы.
Выражение ![]() называется
дифференциалом дуги.
называется
дифференциалом дуги.
Если кривая задана уравнением x=f(y), yÎ[a,b], то, рассуждая аналогично, можно получить формулу
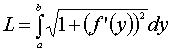 ,
, ![]() .
.
Если
кривая на плоскости задана
параметрически: x=x(t), y=y(t), ![]() ;
; ![]() ,
где x(t), y(t)
– дифференцируемые функции, имеющие
на отрезке
,
где x(t), y(t)
– дифференцируемые функции, имеющие
на отрезке ![]() непрерывную
производную, то, выполнив замену
переменной в предыдущих формулах,
получим:
непрерывную
производную, то, выполнив замену
переменной в предыдущих формулах,
получим:
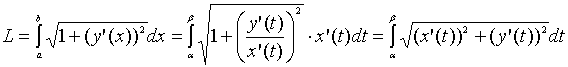 ,
, ![]() .
.
Если задана пространственная кривая параметрическими уравнениями x=x(t), y=y(t), z=z(t), , где x(t), y(t), z(t) – дифференцируемые на отрезке функции с непрерывной производной, то длина кривой вычисляется по формуле
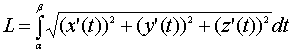 ,
, ![]() .
.
Пусть
в полярных координатах кривая задана
уравнением ![]() ,
где
,
где ![]() -
дифференцируемая функция с непрерывной
на
производной
-
дифференцируемая функция с непрерывной
на
производной ![]() .
Запишем формулы перехода от декартовой
системы координат к полярной:
.
Запишем формулы перехода от декартовой
системы координат к полярной: ![]() .
Если в эти формулы подставить
.
Если в эти формулы подставить ![]() ,
то получится параметрическое задание
кривой, где параметр
,
то получится параметрическое задание
кривой, где параметр ![]() -
полярный угол. Тогда по формуле для
параметрически заданной функции можно
найти длину дуги кривой:
-
полярный угол. Тогда по формуле для
параметрически заданной функции можно
найти длину дуги кривой:
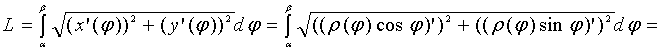
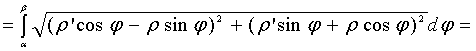
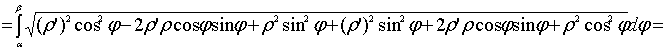
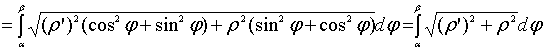 .
.
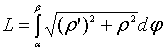 ,
, ![]() .
.
Рассмотрим некоторые примеры вычисления длины дуги кривой.
Пример
1. Вычислить длину дуги кривой 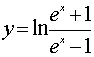 от
точки
от
точки ![]() до
точки
до
точки ![]() ,
(b>a).
,
(b>a).
Решение. Воспользуемся формулой
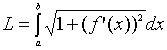 :
:
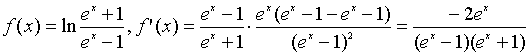 ;
;
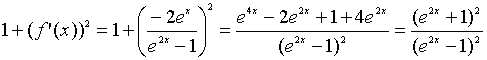 ;
;
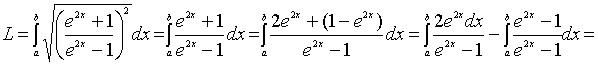
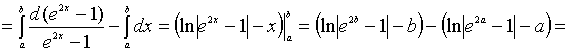
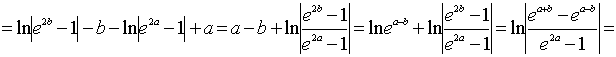
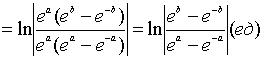 .
.
Пример 2. На циклоиде x=a(t-sint), y=a(1-cost), a>0, найти точку, которая делит первую арку циклоиды по длине в отношении 1:3.
Решение. Первая арка циклоиды соответствует изменению параметра t от t=0 до t=2p. Вычислим длину первой арки циклоиды.
![]() ;
;
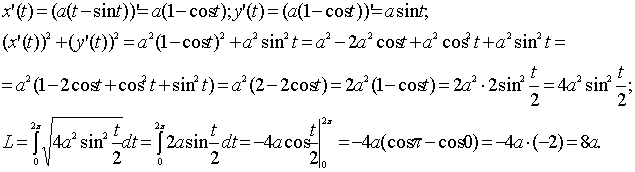
Таким
образом, искомая точка, соответствующая
значению параметра ![]() ,
определяет часть кривой, имеющую длину
2а, то есть
,
определяет часть кривой, имеющую длину
2а, то есть
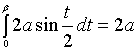 .
.
Найдем
из этого равенства значение ![]() :
:
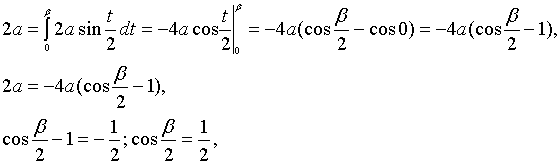
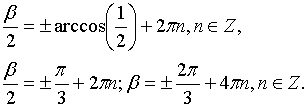
Исходя
из условий задачи, следует выбрать
значение ![]() .
.
Если ![]() ,
то
,
то
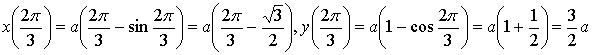 .
.
Искомая точка имеет координаты:
![]() .
.
Пример
3. Найти длину дуги кривой, заданной в
полярных координатах уравнением 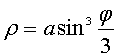 , a>0.
, a>0.
Решение.
Уравнение ![]() , a>0,
определяет замкнутую кривую, соответствующую
изменению j от
0 до 3p (рисунок
8).
, a>0,
определяет замкнутую кривую, соответствующую
изменению j от
0 до 3p (рисунок
8).
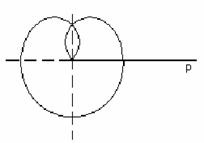
Рисунок 8.
Воспользуемся
формулой 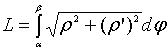 :
:
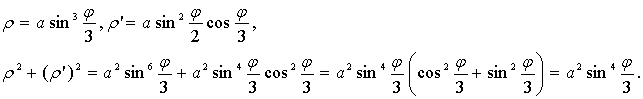
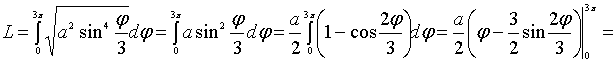
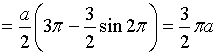 .
.
