164. Что такое функция распределения частиц по энергетическим состояниям?

В (идеальном) ферми-газе в пределе низких температур  . В этом случае (полагая уровни энергии невырожденными  ), функция распределения частиц называется функцией Ферми:

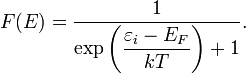
165. Что такое плотность электронных состояний?

Плотность состояний — величина, определяющая количество энергетических уровней в интервале энергий на единицу объёма в трёхмерном случае (на единицу площади — в двумерном случае). Является важным параметром в статистической физике и физике твёрдого тела. Термин может применяться к фотонам, электронам, квазичастицам в твёрдом теле и т. п. Применяется только для одночастичных задач, то есть для систем где можно пренебречь взаимодействием (невзаимодействующие частицы) или добавить взаимодействие в качестве возмущения (это приведёт к модификации плотности состояний).

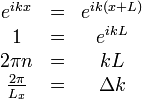
где n — любое целое число, а   — расстояние между состояниями с различными k.

Полное количество k-состояний, доступных для частицы - объем k-пространства доступного для неё, разделенного на объём k-пространства, занимаемого одним состоянием. Доступный объем - просто интеграл от   к  . Объём k-пространства для одного состояния в n-мерном случае запишется в виде

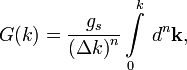
 — вырождение уровня (обычно это спиновое вырождение равное 2). Это выражение нужно продифференцировать, чтобы найти плотность состояний в k-пространстве:  .

166. Что такое функция распределения Бозе–Эйнштейна?

В статистической механике статистика Бо́зе — Эйнште́йна определяет распределениетождественных частиц с нулевым или целочисленным спином (таковыми являются, например, фотоны и атомы гелия-4) по энергетическим уровням в состоянии термодинамического равновесия. В 1924 году она была предложена Шатьендранатом Бозедля описания фотонов. В 1924-1925 Альберт Эйнштейн обобщил её на системы атомов с целым спином.

Согласно статистике Бозе — Эйнштейна, количество частиц в заданном состоянии i, равняется

где  , n_i  — количество частиц в состоянии i, g_i  — вырождение уровня i, ε_i  — энергия состояния i, μ — химпотенциал системы, k — постоянная Больцмана, T — абсолютное значение температуры.

В пределе   статистика Бозе-Эйнштейна переходит в статистику Максвелла — Больцмана, а в пределе   — в распределение Рэлея:

.

167. Что такое функция распределения Ферми–Дирака?

Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелымспином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет распределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии.

Среднее число частиц в состоянии с энергией   есть

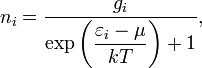
где

 — среднее число частиц в состоянии  ,

 — энергия состояния  ,

 — кратность вырождения состояния   (число состояний с энергией  ),

 — химический потенциал (который равен энергии Ферми   при абсолютном нуле температуры),

 — постоянная Больцмана,

 — абсолютная температура.