Ответы на вопросы

1) Бинарные отношения служат простым и удобным аппаратом для весьма широкого круга задач. Язык бинарных и n-арных отношений используется во многих прикладных (для математики) областях, например, таких как математическая лингвистика, математическая биология, математическая теория баз данных. Широкое использование языка бинарных отношений легко объясняется - геометрический аспект теории бинарных отношений есть попросту теория графов.

Введем необходимые определения.

Определение 1.1. Декартовым произведением множеств X и Y называется множество XxY всех упорядоченных пар (x, y) таких, что x  X, y Y.

Определение 1.2. Соответствием между множествами X и Y (или соответствием из X в Y) называется любое подмножество декартова произведения XxY. Если множества X и Y совпадают, то соответствие между множествами X и Y называют также бинарным отношением на множестве X.

1. Рефлексивность:

2. Слабая рефлексивность:

3. Сильная рефлексивность:

4. Антирефлексивность:

5. Слабая антирефлексивность:

6. Сильная антирефлексивность:

7. Симметричность:

8. Антисимметричность:

9. Асимметричность:

10. Сильная линейность:

11. Слабая линейность:

12. Транзитивность:

2) Так как бинарные отношения являются множествами, то к ним применимы все понятия, которые вводятся для множеств: понятие равенства, включения, а также операции пересечения, объединения и дополнения. В этом разделе мы будем считать, что все отношения заданы на одном и том же множестве X.

Пусть  и  - два бинарных отношения на множестве X. Каждому из них соответствует некоторое множество пар (подмножества   и    ).

Определение 2.1. Пересечением отношений  и , заданных на множестве X, называется отношение такое, что:

Пример 2.1. Пересечением отношений "не меньше" и "не равно", определенных на множестве действительных чисел R, является отношение "строго больше":

    .

 Определение 2.2. Объединением отношений  и , заданных на множестве X, называется отношение , такое, что:

является отношение "быть ребенком".

Определение 2.3. Разностью отношений  и , заданных на множестве X, называется отношение  \, такое, что:

Пример 2.3. Разностью отношений "не меньше" и "не больше" на R является отношение "больше":

 .

Пример 2.4. Разностью отношений "быть ребенком" и "быть дочерью", определенных на множестве всех людей, является отношение "быть сыном".

Определение 2.4. Дополнением отношения  , определенного на множестве X, называется отношение, определяемое подмножеством пар из XxX, не входящих в :

x y .

Пример 2.5. Дополнением отношения "не меньше" на R является отношение "не меньше":

.

Отметим, что приведенные выше определения являются просто перефразировками соответствующих определений для обычных множеств и все свойства теоретико-множественных операций пересечения, объединения и дополнения, имеющие место для произвольных множеств, выполняются и для отношений.

Кроме теоретико-множественных операций для отношений вводятся некоторые дополнительные операции, которые связаны с их специфической структурой. Мы рассмотрим две такие операции.

Определение 2.5. Если в каждой упорядоченной паре, принадлежащей отношению , поменять местами первую и вторую компоненты, то получим новое отношение, которое называется обратным для отношения  и обозначается через ^-1:

.

Свойства отношений

Определение 3.1. Бинарное отношение  на множестве X называется рефлексивным, если для любого элемента a X выполняется условие a  a:

( a X) a a.

Если отношение представлено с помощью графа, то рефлексивность этого отношения означает, что в каждой вершине графа обязательно имеется петля.

Для отношения, заданного с помощью булевой матрицы его рефлексивность равносильна тому, что по главной диагонали этой матрицы (идущей из ее левого верхнего угла в правый нижний) стоят только символы 1.

Определение 3.2. Бинарное отношение  на X называется антирефлексивным, если ни для одного a X не выполняется условие a  a:

( a X)  .

Обозначим через I_x отношение на множестве X, состоящее из пар вида (a, a), где a  X:

I_x = {(a, a)| a  X}.

Отношение I_x обычно называют диагональю множества X или отношением тождества на X.

Очевидно, что отношение  на множестве X рефлексивно, если диагональ I_x является подмножеством множества  :

I_x   .

Отношение антирефлексивно, если диагональ I_x и отношение  не имеют ни одного общего элемента:

I_x   = O.

Определение 3.3. Бинарное отношение  на множестве X называется симметричным, если из a  b следует b  a:

( a, b X)(a b ba).

Примерами симметричных отношений являются:

• отношение перпендикулярности на множестве прямых;

• отношение касания на множестве окружностей;

• отношение "быть похожим" на множестве людей;

• отношение "иметь одинаковый пол" на множестве животных.

• 3) Множество 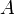является подмножеством множества , если любой элемент, принадлежащий , также принадлежит . Пишут: или 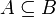. Таким образом,

• Множество в таком случае называется надмно́жеством множества , и этот факт часто записывают: или

Множество называется подмножеством множества если все элементы являются также элементами Любое множество является своим подмножеством: Если при этом , то называется собственным подмножеством По определению полагают, что пустое множество является подмножеством любого множества:

Будем рассматривать множества, элементами которых являются числа. Такие множества называются числовыми. Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление. Наиболее распространенные числовые множества:

• ‑ множество натуральных чисел;

• ‑ множество целых чисел;

• – множество рациональных или дробных чисел;

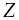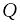• ‑ множество действительных чисел.

Множество всех рациональных чисел является счетным множеством. Счетным является множество всех точек плоскости (пространства) имеющих рациональные координаты.

Множество всех действительных чисел является несчетным: оно имеет мощность, называемую континуумом.

Некоторое непустое подмножество множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число такое, что выполняется неравенство ( ).

Всякое число с указанным свойством называют верхней (нижней) гранью множества .

Непустое подмножество множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.

В противоположность этому определению, множество называется неограниченным сверху (снизу), если какое бы число мы бы не предложили в качестве верхней (нижней) границы множества , всегда найдется элемент этого множества, который будет больше (меньше) .

Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством.

Наименьшую из верхних граней непустого подмножества множества действительных чисел называют точной верхней гранью этого множества и обозначают sup . Наибольшую из нижних граней непустого подмножества множества действительных чисел называют точной нижней гранью этого множества и обозначают inf . Символы sup и inf являются сокращениями от supremum (самый верхний) и infimum (самый нижний).

Примем без доказательства утверждение о том, что всякое ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань.

Граничной точкой множества называется точка, у которой в любом содержащем ее открытом промежутке найдутся как точки, принадлежащие множеству, так и точки, не принадлежащие множеству. Сама граничная точка может, как принадлежать множеству, так и не принадлежать ему.

Граница множества – совокупность граничных точек множества:

• (множество натуральных чисел) ограниченно снизу (например, числом ) и не ограничено сверху;

• (множество действительных чисел) неограничено;

• множество отрицательных чисел неограничено снизу и ограничено сверху.

Соединения. Бином Ньютона

Рассмотрим совокупность различных элементов . Произвольная упорядоченная выборка из этих элементов:

 (   )

4) Объединение множеств

Объединением А В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.

Символическая запись этого определения: А В={х | х А или х В}.

Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз).

Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:

Пересечение множеств

Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств А и В.

Символическая запись этого определения: А ∩ В={х | х А и х В}.

Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:

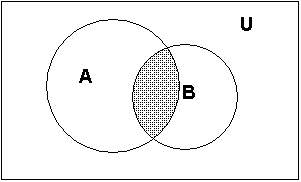
А ∩ В

Дополнение множества

Пусть множество А и В таковы, что А В. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение С_BА=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=С_UА=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей: СА={x | x A}.

На диаграммах Эйлера-Венна можно так пояснить определения С_ВА и СА:

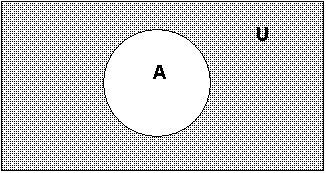
5) Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным.

Два множества и называются эквивалентными, если существует биективное отображение одного множества в другое. Если множества X и Y эквивалентны, то этот факт записывают или и говорят, что множества имеют одинаковые мощности.

Множество называется конечным, если оно эквивалентно множеству при некотором неотрицательном целом . При этом число называется количеством элементов множества , что записывается как .^[1]

В частности, пустое множество является конечным множеством, количество элементов которого равно 0, то есть, .

• Классом эквивалентности элемента 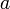называется подмножество элементов, эквивалентных . Из вышеприведённого определения немедленно следует, что, если , то .

Множество всех классов эквивалентности обозначается .

• Для класса эквивалентности элемента используются следующие обозначения: , , .

• Множество классов эквивалентности по отношению является разбиением множества.

6) Определение. Множеством называется совокупность объектов любой природы, которые объединены в одну группу (систему, совокупность) по тем или иным признакам (множество городов, множество положительных чисел, множество студентов, множество действительных чисел и т.д.).      Принадлежность элемента х множеству Х обозначается: х є Х.      Способы записи множеств: А={х₁, х₂,…, х_n}, А= {1, 2, 3, … ,10}, А= {а є R | |a| ≥1}, Х = {х: |x-a|≤b}.      Определение. Множество U образует линейное пространство, если для любых двух его элементов є U и є U определены операция сложения: и операция умножения любого элемента на число: , удовлетворяющие свойствам:         1) ,         2) ,         3) ,         4) ,         5) ,         6) ,         7) ,         8) , где , – нулевой элемент , а коэффициенты α, β, λ, 1 – действительные числа.      Определение. Вектором размерности n называется упорядоченный набор из n действительных чисел. Будем записывать вектор в виде , где - координаты вектора. Размерность вектора определяется числом его координат и является его отличительной характеристикой. Векторы равны, если они одной размерно-сти и имеют равные соответствующие координаты: (2,3,5) = (2,3,5). Нуль-вектор = (0,0,…,0) не следует путать с числом нуль.      Определение. Множество всех векторов размерности n называется арифметическим n-мерным векторным пространством и обозначается Rⁿ.      Экономические величины являются многофакторными (многомерными), и n-мерные векторы служат удобной формой их представления. Например, некоторый набор товаров различных сортов можно охарактеризовать вектором , а соответствующие цены – вектором

Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.

Сложение векторов. Пусть и – два произвольных вектора. Возьмем произвольную точку О и построим вектор ; затем от точки А отложим вектор . Вектор , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается (рис. 1).

 

 

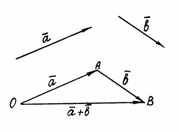
Рис. 1

Ту же сумму можно получить иным способом. Отложим от точки О векторы и . Построим на этих векторах как на сторонах параллелограмм ОАСВ. Вектор – диагональ параллелограмма – является суммой векторов и (рис. 2).

 

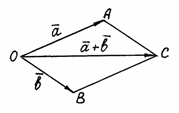
Рис. 2

Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).

 

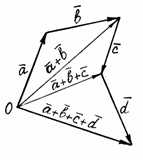
Рис. 3

Вычитание векторов. Разностью векторов и называется такой вектор , который в сумме с вектором дает вектор : Û .

Если векторы и привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).

 

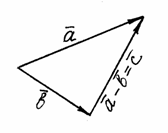
Рис. 4

Таким образом, если на векторах и , отложенных из общей точки О, построить параллелограмм ОАСВ, то вектор , совпадающий с одной диагональю, равен сумме , а вектор , совпадающий с другой диагональю, – разности (рис. 5).

 

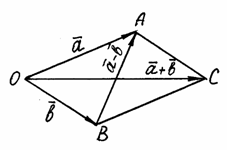
Рис. 5

Умножение вектора на число. Произведением вектора на действительное число называется вектор (обозначают ), определяемый следующими условиями:

1)     ,

2)     при и при .

Очевидно, что при .

Построим, например, векторы и для заданного вектора (рис. 6).

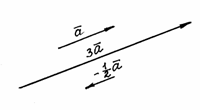
Рис. 6

Из определения следует: два вектора и коллинеарны тогда и только тогда, когда имеет место равенство :

7)

Векторы на координатной плоскости. Обратимся теперь к векторам, лежащим на координатной плоскости хОу. Единичный вектор оси х обозначим через , а координатный вектор оси у обозначим через . Возьмем произвольный вектор iа jаи отложим его от начала координат: =аОА. Сначала рассмотрим общий случай, когда вектор не коллинеарен координатным векторам (рис.1.46).

Рис.1.46

В этом случае точка А не лежит на координатных осях. Опустим из точки А перпендикуляры АА1 на ось х и АА2 на ось у. Получим прямоугольник ОА1АА2. По правилу параллелограмма

ОА=ОА1+ОА2. (11)