Трёхфакторный дисперсионный анализ
Основное
уравнение трёхфакторного дисперсионного
анализа
.
Одинаковое
число повторных опытов
(m=1,2,…,п):
-общая
сумма квадратов разностей наблюдений
и их среднего значения
Промежуточные вычисления, построение вспомогательной таблицы.
Пример. Трёхфакторный эксперимент на двух уровнях с равным числом повторных опытов, n=3
Директор психологического центра решил проанализировать причины, влияющие на эффективность работы отдельных структурных подразделений центра (по городам). В первую очередь, он решил выяснить, зависит ли средний еженедельный объём денежных средств, поступающих от подразделений от уровня квалификации персонала (фактор А), от вида психологической помощи (фактор В), от дня недели (фактор С). Каждый из факторов варьировался первоначально только на двух уровнях: для А-без учёной степени (уровень 1) и со степенью (уровень 2), для В-консультационная (уровень 1) и тренинговая работа (уровень 2), для С-начало недели (уровень 1) и конец недели (уровень 1). Анализ проводился по данным трёх недель наблюдений.
Гипотезы:
1. комплект А.
Н0А: учёная степень не оказывает существенного влияния на объём денежных средств, поступающих от подразделений.
Н1А: учёная степень существенно влияет на объём денежных средств, поступающих от подразделений.
2. комплект В.
Н0В: вид психологической помощи не оказывает существенного влияния на объём денежных средств, поступающих от подразделений.
Н1В: вида психологической помощи существенно влияет на объём денежных средств, поступающих от подразделений.
3. комплект С.
Н0С: триада недели не оказывает существенного влияния на объём денежных средств, поступающих от подразделений.
Н1С: триада недели существенно влияет на объём денежных средств, поступающих от подразделений.
4. комплект АВ.
Н0АВ: учёная степень и вид психологической помощи одновременно не оказывают существенного влияния на объём денежных средств, поступающих от подразделений.
Н1АВ: учёная степень и вид психологической помощи одновременно существенно влияют на объём денежных средств, поступающих от подразделений.
5. комплект АС.
Н0АС: учёная степень и триада недели одновременно не оказывают существенного влияния на объём денежных средств, поступающих от подразделений.
Н1АС: учёная степень и триада недели одновременно существенно влияют на объём денежных средств, поступающих от подразделений.
6. комплект ВС.
Н0ВС: вид психологической помощи и триада недели одновременно не оказывают существенного влияния на объём денежных средств, поступающих от подразделений.
Н1ВС: вид психологической помощи и триада недели одновременно существенно влияют на объём денежных средств, поступающих от подразделений.
7. комплект АВС.
Н0АВС: учёная степень, вид психологической помощи и триада недели одновременно не оказывают существенного влияния на объём денежных средств, поступающих от подразделений.
Н1АВС: учёная степень, вид психологической помощи и триада недели одновременно существенно влияют на объём денежных средств, поступающих от подразделений.
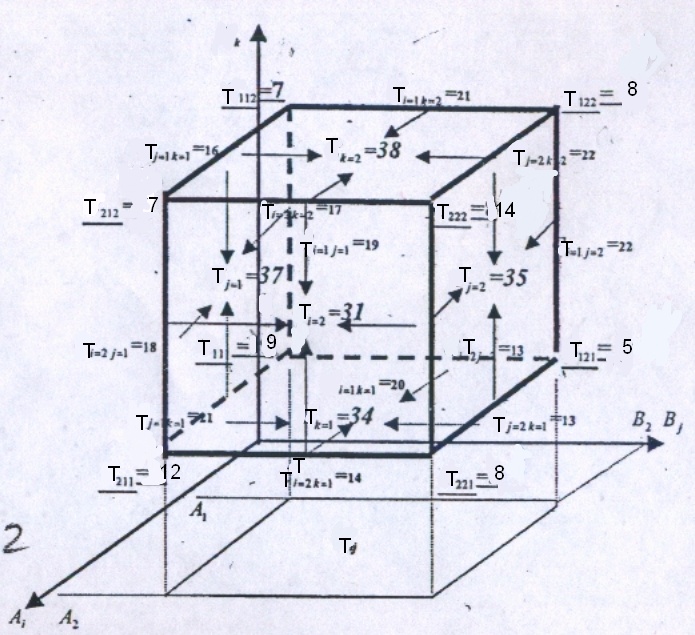
Произведём промежуточные вычисления. С этой целью построим вспомогательную таблицу 13. В таблице разместим данные эксперимента и часть промежуточных вычислений, необходимых для определения сумм квадратов. Для облегчения вычислений изобразим пространство трехфактороного эксперимента на рисунке.
Вычисления.
С=
=
72;
=
=
=216;
=
266;
Ti=1 j=1 = 9 + 9 = 18; Ti=1 j=2 = 5+8 = 13; Ti=2 j=1 = 12+7=19; Ti=2 j=2 = 8+14 = 22;
Ti=1 k=1 = 9+5 = 14; Ti=1 k=2 = 9+8 = 17; Ti=2 k=1 = 12+8 = 20; Ti=2k=2 = 14+7 = 21;
Tj=1k=1 = 9+12= 21; Tj=1k=2= 5+8 = 13; Tj=2k=1 = 12+7=19; Tj=2k=2 = 14+17 = 31;
Ti = 1 =18 +13 =31=17+14; Ti=2 =21+20=41=19+22; Tj = 1=16+ 21 = 37 =18 = 19;
Tj = 2=22+13=35=13+22; Tk=1 =21+13=34=20+14; Tk=2=21+17=38=16 + 22.
Таблица. 13.
Данные об объёме денежных средств, поступающих от подразделений;
Часть промежуточных вычислений.
№ |
АВС |
Xijkm 1*102 y.e |
Tijk |
T2ijk |
Tij |
Ti |
X2 ijkm |
|
||||
1 |
111 |
1 |
3 |
5 |
9 |
81 |
18 |
31 |
1 |
9 |
25 |
35 |
2 |
112 |
2 |
4 |
3 |
9 |
81 |
|
4 |
16 |
9 |
29 |
|
2 |
121 |
2 |
2 |
1 |
5 |
25 |
13 |
4 |
4 |
1 |
9 |
|
4 |
122 |
1 |
5 |
2 |
8 |
64 |
|
1 |
25 |
4 |
30 |
|
5 |
211 |
5 |
3 |
4 |
12 |
144 |
19 |
41 |
25 |
9 |
16 |
50 |
6 |
212 |
4 |
2 |
1 |
7 |
49 |
|
16 |
4 |
1 |
21 |
|
7 |
221 |
3 |
1 |
4 |
8 |
64 |
22 |
9 |
1 |
16 |
26 |
|
8 |
222 |
5 |
4 |
5 |
14 |
196 |
|
25 |
16 |
25 |
66 |
|
|
23 |
24 |
25 |
C=72 |
704 |
72 |
72 |
85 |
84 |
97 |
C0 = 266 |
|
Вычисления в пространстве трехфакторного дисперсионного анализа.
