16.Изобарический и изохорические процессы, теплоемкость в таких процессах

Изобарный процесс -  термодинамический процесс, происходящий в системе при постоянном давлении и массе идеального газа. Согласно закону Гей-Люссака, при изобарном процессе в идеальном газе .

Работа, совершаемая газом при расширении или сжатии газа, равна A = PΔV.

Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии: δQ = ΔI = ΔU + PΔV.

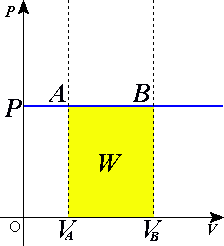График изобарического расширения газа от объёма V_a до V_b. AB здесь является изобарой.

Молярная теплоёмкость при постоянном давлении обозначается как C_p. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера C_p = C_v + R.

Молекулярно-кинетическая теория позволяет вычислить приблизительные значения молярной теплоёмкости для различных газов через значение универсальной газовой постоянной: для одноатомных газов , то есть около 20.8 Дж/(моль·К); для двухатомных газов , то есть около 29.1 Дж/(моль·К); для многоатомных газов C_p = 4R, то есть около 33.3 Дж/(моль·К).

Изохорический или изохорный процесс -это термодинамический процесс, который происходит при постоянном объёме. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма.

Теплоемкость

17.Изотермический и адиабатический процессы: реализация, работа и уравнения

Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре.

Для осуществления изотермического процесса систему обычно помещают в термостат, теплопроводность которого велика, так что теплообмен с системой происходит достаточно быстро по сравнению со скоростью протекания процесса, и, температура системы в любой момент практически не отличается от температуры термостата. Графиком изотермического процесса является изотерма.

В идеальном газе при изотермическом процессе произведение давления на объём постоянно (закон Бойля-Мариотта). Изотермы идеального газа в координатах p,V — гиперболы, расположенные на графике тем выше, чем выше температура, при которой происходит процесс .

При изотермическом процессе системе, вообще говоря, сообщается определённое количество теплоты (или она отдаёт теплоту) и совершается внешняя работа. Альтернативный процесс, при котором теплообмен с окружающей средой отсутствует (термодинамическая система находится в энергетическом равновесии — система не поглощает и не выделяет тепло), называется адиабатическим процессом.

Работа, совершенная идеальным газом в изотермическом процессе, равна , где  — число частиц газа,  — температура, и  — объём газа в начале и конце процесса,  — постоянная Больцмана .

В твёрдом теле и большинстве жидкостей изотермические процессы очень мало изменяют объём тела, если только не происходит фазовый переход.

Первый закон термодинамики для изотермического процесса в идеальном газе записывается в виде:    

Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии. В общем случае адиабатический процесс необратим.

Линия, изображающая адиабатный процесс на какой-либо термодинамической диаграмме, называется адиабатой.

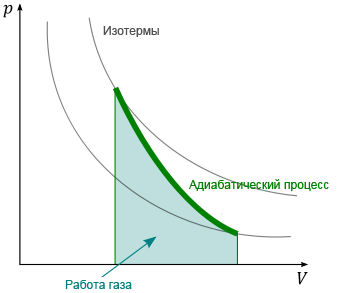
Для адиабатического процесса первое начало термодинамики в силу отсутствия теплообмена (ΔQ = 0) системы со средой имеет вид , где: — изменение внутренней энергии тела, — работа, совершаемая системой, — теплота, полученная системой

Основное уравнение термодинамики применительно к адиабатическому процессу записывается в дифференциалах как ,

где — дифференциальное выражение для работы, a_i — внешние параметры, A_i — соответствующие им внутренние параметры. В частном случае, когда работа совершается через изменение объёма, , где p — давление.

Для идеальных газов адиабата имеет простейший вид и определяется уравнением: , где: — давление газа, — его объём, — показатель адиабаты, и — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

Показатель адиабаты: Для нерелятивистского невырожденного одноатомного идеального газа , для двухатомного , для трёхатомного , для газов состоящих из более сложных молекул, показатель адиабаты, определяется числом степеней свободы конкретной молекулы.

При адиабатическом процессе показатель адиабаты равен , где R — универсальная газовая постоянная.

С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду:

, где T — абсолютная температура газа.

Или к виду:

Поскольку всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (т.е. при уменьшении V) газ нагревается (T возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов.