9.Момент инерции, момент сил, закон вращательного движения

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения СИ: кг·м².

При движении тела по окружности возникает также нормальное или центростремительное ускорение, модуль которого есть

Разобьем вращающееся тело на малые элементы Δmi. Расстояния до оси вращения обозначим через ri, модули линейных скоростей – через υi. Тогда кинетическую энергию вращающегося тела можно записать в виде:

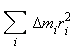Физическая величина зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:

 

В пределе при Δm → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в СИ – килограмм-метр в квадрате (кг∙м2). Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде

Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

В системе СИ единицами измерения для момента силы является ньютон-метр. Символ момента силы M . Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси вращения рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, это то же самое, что сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:

где  — сила, действующая на частицу, а  — радиус-вектор частицы.

10.Термодинамическое уравнение состояния идеального газа

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где  — давление,  — молярный объём,  — универсальная газовая постоянная,  — абсолютная температура,К

Так как , где  — количество вещества, а , где  — масса,  — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта.

 — Закон Гей-Люссака.

 — закон Шарля (второй закон Гей-Люссака, 1808 г.)