- •1.Кинематика. Перемещение, скорость, ускорение.
- •2.Законы Ньютона
- •3.Закон сохранения импульса
- •4.Работа, кинетическая энергия
- •5.Потенциальные силы, потенциальная энергия, закон сохранения энергии
- •6.Гравитационное поле, потенциальная энергия гравитационного поля
- •7.Центральный удар, абсолютно упругий и абсолютно неупругий удар
- •8.Вращательное движение, угловая скорость, угловое ускорение
- •9.Момент инерции, момент сил, закон вращательного движения
- •10.Термодинамическое уравнение состояния идеального газа
- •11.Кинетическое уравнение состояния идеального газа, внутренняя энергия
- •12.Барометрическая формула Больцмана
- •13.Распределение Максвелла
- •14.Броуновское движение
- •15.Первое начало термодинамики. Работа, теплота ,внутренняя энергия.
- •16.Изобарический и изохорические процессы, теплоемкость в таких процессах
- •17.Изотермический и адиабатический процессы: реализация, работа и уравнения
- •18.Второе начало термодинамики, формулировки Томпсона и Клаузиуса
- •19.Цикл Карно
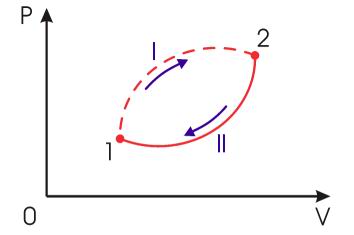
- •Описание цикла Карно:
- •20.Энтропия: определение, закон возрастания энтропии
- •21.Процессы переноса, законы Фика и Фурье
- •22.Закон Кулона, напряженность электрического поля, закон суперпозиции
- •23.Опыт Милликена, заряд электрона.
- •24.Поле электрического диполя
- •25.Теорема Гаусса, примеры ее применения
- •26.Потенциал электрического поля
- •27.Проводники и диэлектрики во внешнем поле
- •28.Диэлектрики, диэлектрическая проницаемость, восприимчивость и вектор поляризации
- •29.Электрическое поле на границе диэлектриков
- •30.Электрическая ёмкость проводника, конденсатор
- •31.Энергия электрического поля
Описание цикла Карно:
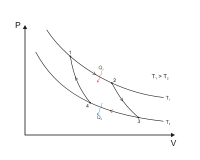
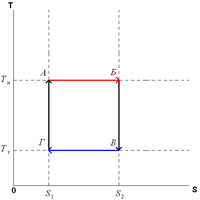
Цикл Карно в координатах P и V Цикл Карно в координатах T и S
Пусть тепловая машина состоит из нагревателя с температурой TH, холодильника с температурой TX и рабочего тела.
Цикл Карно состоит из четырёх стадий:
Изотермическое расширение (на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуру TH, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты QH. При этом объём рабочего тела увеличивается.
Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
Изотермическое сжатие (на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуру TX, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты QX.
Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.
При
изотермических процессах температура
остаётся постоянной, при адиабатических
отсутствует теплообмен, а значит,
сохраняется энтропия (поскольку
![]() при
δQ = 0). Поэтому
цикл Карно удобно представить в
координатах T и S (температура
и энтропия).
при
δQ = 0). Поэтому
цикл Карно удобно представить в
координатах T и S (температура
и энтропия).
20.Энтропия: определение, закон возрастания энтропии
Энтропия — это сокращение доступной энергии вещества в результате передачи энергии. Первый закон термодинамики гласит, что энергию невозможно создать или уничтожить. Следовательно, количество энергии во вселенной всегда такое же, как было и при ее создании. Второй закон термодинамики гласит, что коэффициент полезного действия ни одного реального (необратимого) процесса не может быть 100% при преобразовании энергии в работу.
Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.
![]() ,
,
где dS — приращение энтропии; δQ — минимальная теплота подведенная к системе; T — абсолютная температура процесса;
Применим неравенство Клаузиуса для описания необратимого кругового термодинамического процесса, изображенного на рис 3.13.
|
Рис. 3.13. Необратимый круговой термодинамический процесс |
Пусть
процесс
![]() будет
необратимым, а процесс
будет
необратимым, а процесс
![]() -
обратимым. Тогда неравенство Клаузиуса
для этого случая примет вид:
-
обратимым. Тогда неравенство Клаузиуса
для этого случая примет вид:
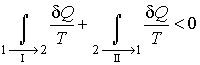
Так
как процесс
является
обратимым, для него можно воспользоваться
соотношением (3.53),
которое дает :
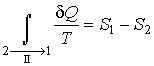
Подстановка
этой формулы в неравенство (3.55)
позволяет получить выражение :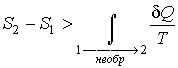
|
|
Сравнение выражений
позволяет записать следующее неравенство
:![]() ,
в котором знак равенства имеет место
в случае, если процесс
,
в котором знак равенства имеет место
в случае, если процесс
![]() является
обратимым, а знак больше, если процесс
-
необратимый.
является
обратимым, а знак больше, если процесс
-
необратимый.
Если
рассмотреть адиабатически изолированную
термодинамическую систему, для которой
![]() ,
то выражение примет вид
,
то выражение примет вид
![]() или
в интегральной форме
или
в интегральной форме
![]()
Полученные неравенства выражают собой закон возрастания энтропии, который можно сформулировать следующим образом: «В адиабатически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс»
Записанное утверждение является ещё одной формулировкой второго начала термодинамики.
Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия.