36.Поток вектора напряженности гравитационного поля. Теорема Гаусса

Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.

Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля (см. ниже).

Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния^[1] в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически).

В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.

Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.

поток напряженности гравитационного поля

.

Здесь: G – напряженность гравитационного поля, S – замкнутая поверхность, внутри которой находится масса т, создающая G-поле. При этом поток напряженности выражается теоремой Остроградского – Гаусса для гравиротационного (GR) поля. ,

где γ – гравитационная постоянная для данного пространства. (Здесь и ниже используется система СИ).

37. Гравитацио́нный потенциа́л — скалярная функция координат и времени, характеризующая гравитационное поле в классической механике. Имеет размерность квадрата скорости, обычно обозначается буквой . Гравитационный потенциал равен отношению потенциальной энергии материальной точки, помещённой в рассматриваемую точку гравитационного поля, к массе этой точки. Впервые понятие гравитационного потенциала ввёл в науку Адриен Мари Лежандр в конце XVIII века.

• В современных теориях гравитации роль гравитационного потенциала играют обычно тензорные поля. Так, в стандартной в наше время теории гравитации — общей теории относительности — роль гравитационного потенциала играет метрический тензор.

Гравитационный потенциал точечной частицы равен: , где  — гравитационная постоянная,  — масса частицы,  — расстояние от частицы. Эта же формула справедлива и для гравитационного потенциала любого тела со сферически-симметричным распределением плотности массы внутри него.Для тела с произвольным распределением плотности массы гравитационный потенциал удовлетворяет уравнению Пуассона: , где  — оператор Лапласа,  — объёмная плотность распределения массы в рассматриваемой точке. Общее решение этого уравнения имеет вид: где r — расстояние от элемента объёма dV до рассматриваемой точки поля, а интегрирование производится по всему объёму тел, создающих поле. Гравитационный потенциал симметричного тела симметричен.

38. Гравитационное поле точечной массы

Нахождение аномалий силы тяжести, создаваемых телами известной формы, составляет прямую задачу гравиметрии. В основе аналитического способа решения прямой задачи лежит известный закон всемирного тяготения Ньютона, согласно которому притяжение единичной массы (весом 1 г) элементарной массой равно .      (V.4) Положим, что точка с массой dm находится на расстоянии r от пункта наблюдения и на глубине h от поверхности Земли (рис. 26). Потенциал точки будет ,      (V.5) где , т.е. 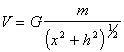.    (V.6) Из определения силы тяжести (см. гл. 4, §3) ее вертикальная и горизонтальная составляющие определяются как первая и вторая производные по h и x: ;     (V.7) .        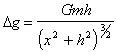(V.8) ;   (V.9) 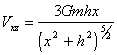.     (V.10) Максимальное и минимальное значение Dg принимает при x = 0 и x = ±¥: .        (V.11) .               (V.12)

39.Электромагни́тное по́ле — фундаментальное физическое поле, взаимодействующее с электрически заряженными телами, представляющее собой совокупность электрического и магнитного полей, которые могут ,при определённых условиях, порождать друг друга.

Электромагнитное поле (и его изменение со временем) описывается в электродинамике в классическом приближении посредством системы уравнений Максвелла. При переходе от одной инерциальной системы отсчета к другой электрическое и магнитное поле в новой системе отсчета — каждое зависит от обоих — электрического и магнитного — в старой, и это ещё одна из причин, заставляющая рассматривать электрическое и магнитное поле как проявления единого электромагнитного поля.

В современной формулировке электромагнитное поле представлено тензором электромагнитного поля, компонентами которого являются три компоненты напряжённости электрического поля и три компонента напряжённости магнитного поля (или — магнитной индукции)^[1], а также четырёхмерным электромагнитным потенциалом — в определённом отношении ещё более важным.

Действие электромагнитного поля на заряженные тела описывается в классическом приближении посредством силы Лоренца.

Квантовые свойства электромагнитного поля и его взаимодействия с заряженными частицами (а также квантовые поправки к классическому приближению) — предмет квантовой электродинамики, хотя часть квантовых свойств электромагнитного поля более или менее удовлетворительно описывается упрощённой квантовой теорией, исторически возникшей заметно раньше.

Возмущение электромагнитного поля, распространяющееся в пространстве, называется электромагнитной волной (электромагнитными волнами)^[2]. Любая электромагнитная волна распространяется в пустом пространстве (вакууме) с одинаковой скоростью — скоростью света (свет также является электромагнитной волной). В зависимости от длины волны электромагнитное излучение подразделяется на радиоизлучение, свет (в том числе инфракрасный и ультрафиолет), рентгеновское излучение и гамма-излучение.

Теперь можно перейти к существу вопроса об электрическом (точнее пока об электростатическом) поле. Наши представления о том, что такое электрическое поле, образуются в результате опытного исследование его свойств. Иным путем эти свойства не могут быть найдены. Главное свойство электрического поля — это способность действовать на электрические заряды (как неподвижные, так и движущиеся) с некоторой силой. По действию на заряд устанавливается присутствие поля, распределение его в пространстве, изучаются все его характеристики.

Основное свойство магнитного поля — способность его действовать на движущиеся электрические заряд с определенной силой. Создается магнитное поле так же только движущимися электрическими зарядами. Силовые линии магнитного поля охватывают ток в виде замкнутых линий, не имеющих ни начала, ни конца.

40. Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году.

Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с. Заряд в один кулон очень велик. Если бы два носителя заряда (q₁ = q₂ = 1 Кл) расположили в вакууме на расстоянии 1 м, то они взаимодействовали бы с силой 9·10⁹ H.

Совокупность всех известных экспериментальных фактов позволяет выделить следующие свойства заряда:

• Существует два рода электрических зарядов, условно названных положительными и отрицательными. Положительно заряженными называют тела, которые действуют на другие заряженные тела так же, как стекло, наэлектризованное трением о шелк. Отрицательно заряженными называют тела, которые действуют так же, как эбонит, наэлектризованный трением о шерсть. Выбор названия «положительный» для зарядов, возникающих на стекле, и «отрицательный» для зарядов на эбоните совершенно случаен.

• Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

• Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

• Важным свойством электрического заряда является его дискретность. Это означает, что существует некоторый наименьший, универсальный, далее не делимый элементарный заряд, так что заряд q любого тела является кратным этому элементарному заряду:

,

где N – целое число, е – величина элементарного заряда. Согласно современным представлениям, этот заряд численно равен заряду электрона e = 1,6∙10^-19 Кл. Поскольку величина элементарного заряда весьма мала, то для большинства наблюдаемых и используемых на практике заряженных тел число N очень велико, и дискретный характер изменения заряда не проявляется. Поэтому считают, что в обычных условиях электрический заряд тел изменяется практически непрерывно.

• Закон сохранения электрического заряда.

Внутри замкнутой системы при любых взаимодействиях алгебраическая сумма электрических зарядов остается постоянной:

.

Изолированной (или замкнутой) системой мы будем называть систему тел, в которую не вводятся извне и не выводятся из нее электрические заряды.

Нигде и никогда в природе не возникает и не исчезает электрический заряд одного знака. Появление положительного электрического заряда всегда сопровождается появлением равного по модулю отрицательного заряда. Ни положительный, ни отрицательный заряд не могут исчезнуть в отдельности, они могут лишь взаимно нейтрализовать друг друга, если равны по модулю.

Так элементарные частицы способны превращаться друг в друга. Но всегда при рождении заряженных частиц наблюдается появление пары частиц с зарядами противоположного знака. Может наблюдаться и одновременное рождение нескольких таких пар. Исчезают заряженные частицы, превращаясь в нейтральные, тоже только парами. Все эти факты не оставляют сомнений в строгом выполнении закона сохранения электрического заряда.

Причина сохранения электрического заряда до сих пор пока неизвестна.