9. Полярные координаты.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.

Д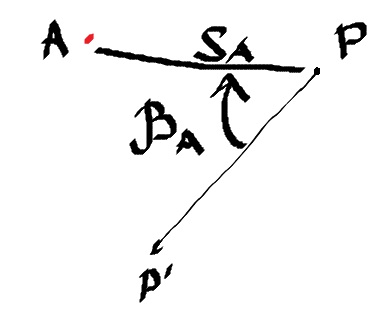 ля полярной системы координат характерно наличие полюса P, полярной оси РР’ , полярного угла β между направлением полярной оси и направлением на определяемую точку, расстояния S (горизонтального проложения - проекции линии местности на горизонтальную плоскость.) В математике горизонтальное проложени называют радиусом –вектором. Точка Р’ , как и полюс, является точкой с известными координатами. То есть полярная ось однозначно задана на местности. Полярные углы отсчитывают от полярной оси по движению часовой стрелки или против него.

В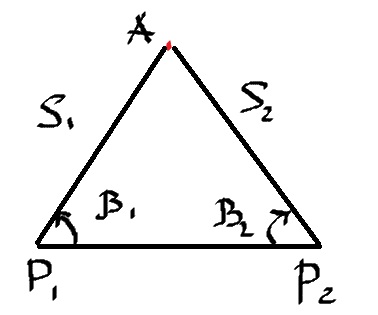 биполярной системе координат имеется два полюса (Р₁ и Р₂), а положение точки определяется значениями двух горизонтальных полярных углов β1 и β2 (угловая засечка), либо значениями двух измеренных горизонтальных проложений S1 и S2 (линейная засечка). Надо заметить что угол β1 отсчитывается против хода часовой стрелки, а угол β2 по ходу часовой стрелки.

10. Связь прямоугольной и полярной систем координат (прямая и обратная геодезические задачи.)

Прямая геодезическая задача на плоскости

В геодезии есть две стандартные задачи: прямая геодезичеcкая задача на плоскости и обратная геодезическая задача на плоскости.

Прямая геодезическая задача - это вычисление координат X2, Y2 второго пункта, если известны координаты X1, Y1 первого пункта, дирекционный угол α и длина S линии, соединяющей эти пункты.

Обратная геодезическая задача на плоскости

Обратная геодезическая задача - это вычисление дирекционного угла α и длины S линии, соединяющей два пункта с известными координатами X1, Y1 и X2

 

 

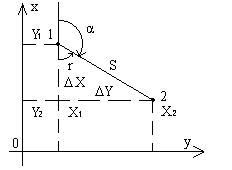
Построим на отрезке 1-2 как на гипотенузе прямоугольный треугольник с катетами, параллельными осям координат. В этом треугольнике гипотенуза равна S, катеты равны приращениям координат точек 1 и 2 ( ΔX = X2 - X1, ΔY = Y2 - Y1 ), а один из острых углов равен румбу r линии 1-2.

Если Δ X  00 и Δ Y  00, то решаем треугольник по известным формулам:

              

             

Для данного рисунка направление линии 1-2 находится во второй четверти, поэтому на основании (1.22) находим:

              

Общий порядок нахождения дирекционного угла линии 1-2 включает две операции:

- определение номера четверти по знакам приращений координат Δ>X и ΔY

- вычисление α по формулам в соответствии с номером четверти.

Контролем правильности вычислений является выполнение равенства:

          (2.12)

Если ΔX = 0.0 , то

S = іΔYі;  и α = 90o 00' 00" при ΔY > 0 ,  α = 270o 00' 00" при ΔY < 0 .

Если ΔY = 0.0 , то

S = іΔXі  и α = 0o 00' 00" при ΔX > 0 ,  α = 180o 00' 00" при ΔX < 0 .

Для решения обратной задачи в автоматическом режиме (в программах для ЭВМ) используется другой алгоритм, не содержащий тангенса угла и исключающий возможное деление на ноль:

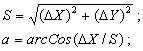            (2.13)

если ΔY => 0o , то α = a ,  если ΔY < 0o , то α = 360o - a.

11.Ориентирные углы направлений (азимут, дирекционный угол и румб).

Азимут - угол между направлением на север (в Южном полушарии — на юг) и направлением на какой-либо удалённый предмет. Отсчитывается обычно по часовой стрелке.

Румб – острый горизонтальный угол, отсчитываемый от ближайшего направления меридиана до данной линии. Румбы имеют значения от 0 до 90 градусов и сопровождаются названием четверти, в которой проходит линия.

В геодезии и топографии применяется также ориентирование линий относительно осевого меридиана. Угол отсчитываемый от северного направления меридиана до данного направления по ходу часовой стрелки, называется дирекционным углом.