8.3.3 Цифровые компараторы.

Цифровой компаратор предназначен для сравнения двух n-разрядных двоичных чисел A={a₁, a₂, ..., a_n} и B={b₁, b₂, ..., b_n}. В результате сравнения может установливаться одно из соотношений: =, ≠; >; <; ≥; ≤. Выходная функция F принимает единичное значение, если проверяемое соотношение выполняется или нулевое – если не выполняется. Цифровой компаратор позволяет реализовывать ту часть алгоритма измерения в цифровой измерительной технике, в которой заложена процедура сравнения неизвестного значения измеряемой величины с цифровой мерой. Рассмотрим синтез компаратора для реализации функции равенства двух n-разрядных двоичных кодов. Факты равенства, больше и меньше отдельных разрядов определим функциями f_(A=B)i, f_(A>B)i и f_(A<B)i, заданной следующей таблицей истинности 8.9:

Таблица 8.9.

Входы		Выходы
ai	bi	f(A=B)i	f(A>B)i	f(A<B)i
0	0	1	0	0
0	1	0	0	1
1	0	0	1	0
1	1	1	0	0

Тогда факт неравенства разрядов будет определяться инверсным значением функции . Определим ФАЛ для f_(A=B)i, соответствующую приведенной таблице истинности

.

Синтезированная структурная схема в соответствии с формулой для f_(A=B)i имеет вид, представленный рис. 8.22.

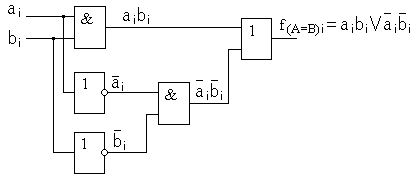
Рис. 8.22. Функциональная схема устройства сравнения одноразрядных кодов.

Выполним следующие преобразования над функцией f_(A=B)i, используя тождества алгебры логики:

,

т.е. окончательно имеем инверсию функции исключающее ИЛИ.

Функция неравенства одного разряда тогда будет выражаться через прямое значение функции Исключающее ИЛИ. Для перехода от равенства (неравенства) отдельных разрядов к функции равенства F_(A=B) (неравенства ) всего n-разрядного кода необходимо установить факт наличия логических единиц во всех функциях f_(A=B)i ( ). Это осуществляется n-входовым элементом И. ФАЛ для функции F_(A=B) с учетом использования функции инверсии исключающего ИЛИ имеет вид

.

Функция f_(A>B)i одноразрядного числа согласно таблице 8.9 будет реализовываться двухвходовым элементом И, на один вход которого будет подаваться разряд a_i в прямом виде, а на второй – разряд в инверсном виде, т.е. . Несколько сложнее обстоит дело со схемой сравнения n-разрядных слов на «больше». Для этого анализ неравенства должен выполняться последовательно в направлении от старших разрядов в сторону младших. Младшие разряды сравниваются при условии равенства старших. Тогда логика сравнения на «больше» для двухразрядного слова с учетом равенства/неравенства старшего разряда может быть представлена в следующем виде

.

Аналогично можно записать логику сравнения для трехразрядного числа

и четырехразрядного числа

.

В общем случае функция сравнения на «больше» для произвольного n-разрядного числа можно выразить

Подставив минтермы функций f_(A>B)i в переменных a_i и b_i и эквивалентные функциям f_(A=B)i элементы исключающее ИЛИ-НЕ, можно реализовать представленную ФАЛ для F_(A>B).

Функцию сравнения на «меньше» можно определить как

,

т.е. только если будет отсутствовать факт равенства F_(A=B)=0 и факт больше F_(A>B)=0, то схемой совпадения нулей (функцией ИЛИ) установится общий ноль, а инверсия этого нуля даст единичное значение функции F_(A<B) как последнего оставшегося варианта сравнения.

Пример схемы, реализующей рассмотренные выше функции F_(A=B), F_(A>B) и F_(A<B) двух четырехразрядных чисел приведен на рис.8.23.

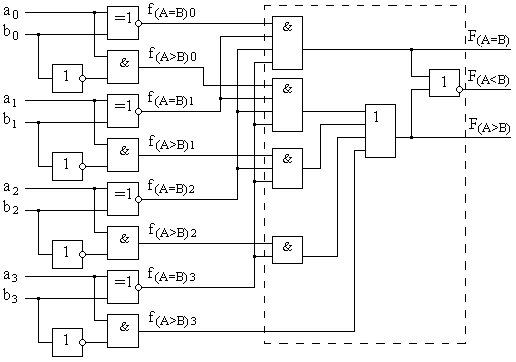
Рис.8.23. Функциональная схема компаратора, реализующего функции «равно», «больше», «меньше» двух четырехразрядных чисел.

Из-за громоздкости структуры компараторов чисел большой разрядности и необходимости использования в этом случае логических элементов с большим количеством входов, в интегральном исполнении обычно реализуются компараторы, сравнивающие двоичные коды с разрядностью n не более 4 или 8 бит. Для повышения разрядности обрабатываемых кодов сравниваемые слова разбиваются на группы фиксированной разрядности с индивидуальными выходами функций сравнения на «равно» F_(A=B)i и «больше» F_(A>B)i в каждой группе. Тогда описанный выше метод применим и для анализа n-разрядных кодов. Для этого выходы функций равенства и больше компараторов отдельных групп объединяются в часть схемы рис.8.23, заключенную в пунктирную линию. В результате формируется результат сравнения кодов всей длины. В условном графическом обозначении функция компаратора задается символами «= =» или «COMP».

В качества примера можно привести микросхему четырехразрядного компаратора К561ИП2, реализующую функции сравнения на «больше», «меньше» и «равно». Эта микросхема может также применяться для сравнения кодов большей разрядности (рис.8.24). Для этого в ней предусмотрены входы переноса функций «меньше» и «равно», на которые подаются выходы одноименных функций группы младших разрядов. Вход «больше» в данной микросхеме избыточен, и на него в микросхемах всех групп необходимо постоянно подавать потенциал логической единицы. На вход «меньше» микросхемы самой младшей группы необходимо подать логический ноль, а на вход «равно» - логическую единицу. Такое же включение микросхемы должно быть и при использовании ее для сравнения четырехразрядных слов.

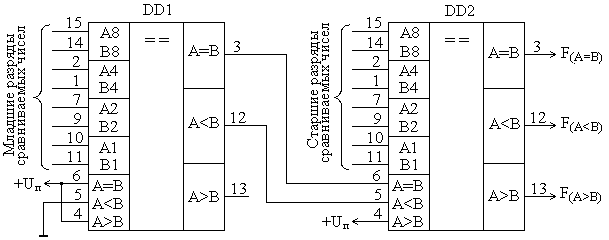
Рис.8.24. Включение микросхемы К561ИП2 при повышения разрядности сравниваемых слов.