
- •43. Нестационарные временные ряды. Метод разностей и интегрируемость.
- •44. Оценка порядка интегрируемости. Тесты на единичный корень. Интеграционная статистика Дарбина-Уотсона
- •45. Оценка порядка интегрируемости. Тесты Дики-Фуллера
- •46. Модификации теста Дики-Фуллера для случая автокорреляции
- •47. Модели arima. Идентификация модели и оценивание пар-ров.
- •48.Общая хар-ка моделей с распределенным лагом и моделей авторегрессии. Интерпретация пар-ов моделей с распределенным лагом и моделей авторегрессии.
- •49.Изучение структуры лага и выбор вида модели с распределенным лагом. Модели Алмон.
- •50. Изучение структуры лага и выбор вида модели с распределенным лагом. Метод Койка
- •51. Панельные данные. Анализ двухпериодной модели.
- •52.Панельные данные. Обобщение на более чем два периода наблюдений
47. Модели arima. Идентификация модели и оценивание пар-ров.
Пусть Xt — нестац-ный процесс со стац-ными разностями d-го порядка, т.е. Yt=dXt - стац процесс, а d-1Xt — нестац, т.е Xt - интегрируем d-го порядка.
Если Yt
уже стац-ый (процесс ARMA(p, q)), т.е.
![]() (1) тогда
Xt
называется процессом
ARIMA(p,d,q), т.е
интегр-мым авторегрессионным процессом
скользящего среднего, где p-порядок
авторегр-ого процесса, q-порядок
max
лага для скольз среднего, d-порядок
интегр-ти. Зам:
Свободный член φ0
приравнивается к нулю (опускается).
Большинство эмпирических ВР можно
считать реализациями процессов ARIMA.
Основная задача в анализе ВР —
специфицировать порядок модели
ARIMA(p,d,q), т.е определить пар-ры p,d,q по
св-вам ВР и оценить пар-ры ур-ния модели
и дисперсию остатков. Идентификация
модели и оценивание параметров.
Моделирование
состоит из следующих шагов. Шаг
1. Диагностика,
т.е. проверка ВР на стац-ть, условие
эргодичности: – анализ графика ВР; –
Тест на единичный корень; – В случае
нестационарности - взятие разностей и
повтор тестов; – Оценивание
автокорреляционной ф-ции (ACF).
Шаг 2.
Выбор типов возможных процессов,
сгенерировавших этот ВР (идентификация
модели). В рез-те д.б. получены три осн
пар-ра: d — порядок интегр-ти, р и q —
порядки компонент AR и МА соотв-но. Пар-р
d легко определяется как кол-во взятых
разностей, необходимое для получения
стац-ого процесса. В случае сомнений
следует выбирать модели с наименьшим
возможным числом пар-ров. Шаг
3. Оценивание
пар-ров для всех возможных модели
подходящими статистическими методами:
– обычный МНК; – метод максимального
правдоподобия (МПМ); – метод минимизации
квадратов ошибок прогноза. Шаг
4. Выбор
наиболее подходящей модели среди
оцененных: – анализ остатков, которые
д. иметь св-ва белого шума; – рассмотрение
модели, наилучшим образом воспроизводящей
конкретный ВР, и ее наиболее экономичною
с точки зрения кол-ва пар-ров. При
сравнении различных моделей для одного
и того же ВР имеем дело с несколькими
конкурирующими целями: 1. для МНК —
минимизация дисперсии ошибок и минимизация
числа пар-ров модели; 2. для МПМ —
максимизация ф-ции правдоподобия при
минимизация числа пар-ров модели. Обычно
оцениваемая модель лучше соотв-ет ВР
при более высоких порядках p
и q модели ARMA, но это приводит к усложнению
модели. Для нахождения компромисса
используются информационный критерий
Акаики и критерий Шварца. Кр. Акаики:
(1) тогда
Xt
называется процессом
ARIMA(p,d,q), т.е
интегр-мым авторегрессионным процессом
скользящего среднего, где p-порядок
авторегр-ого процесса, q-порядок
max
лага для скольз среднего, d-порядок
интегр-ти. Зам:
Свободный член φ0
приравнивается к нулю (опускается).
Большинство эмпирических ВР можно
считать реализациями процессов ARIMA.
Основная задача в анализе ВР —
специфицировать порядок модели
ARIMA(p,d,q), т.е определить пар-ры p,d,q по
св-вам ВР и оценить пар-ры ур-ния модели
и дисперсию остатков. Идентификация
модели и оценивание параметров.
Моделирование
состоит из следующих шагов. Шаг
1. Диагностика,
т.е. проверка ВР на стац-ть, условие
эргодичности: – анализ графика ВР; –
Тест на единичный корень; – В случае
нестационарности - взятие разностей и
повтор тестов; – Оценивание
автокорреляционной ф-ции (ACF).
Шаг 2.
Выбор типов возможных процессов,
сгенерировавших этот ВР (идентификация
модели). В рез-те д.б. получены три осн
пар-ра: d — порядок интегр-ти, р и q —
порядки компонент AR и МА соотв-но. Пар-р
d легко определяется как кол-во взятых
разностей, необходимое для получения
стац-ого процесса. В случае сомнений
следует выбирать модели с наименьшим
возможным числом пар-ров. Шаг
3. Оценивание
пар-ров для всех возможных модели
подходящими статистическими методами:
– обычный МНК; – метод максимального
правдоподобия (МПМ); – метод минимизации
квадратов ошибок прогноза. Шаг
4. Выбор
наиболее подходящей модели среди
оцененных: – анализ остатков, которые
д. иметь св-ва белого шума; – рассмотрение
модели, наилучшим образом воспроизводящей
конкретный ВР, и ее наиболее экономичною
с точки зрения кол-ва пар-ров. При
сравнении различных моделей для одного
и того же ВР имеем дело с несколькими
конкурирующими целями: 1. для МНК —
минимизация дисперсии ошибок и минимизация
числа пар-ров модели; 2. для МПМ —
максимизация ф-ции правдоподобия при
минимизация числа пар-ров модели. Обычно
оцениваемая модель лучше соотв-ет ВР
при более высоких порядках p
и q модели ARMA, но это приводит к усложнению
модели. Для нахождения компромисса
используются информационный критерий
Акаики и критерий Шварца. Кр. Акаики:
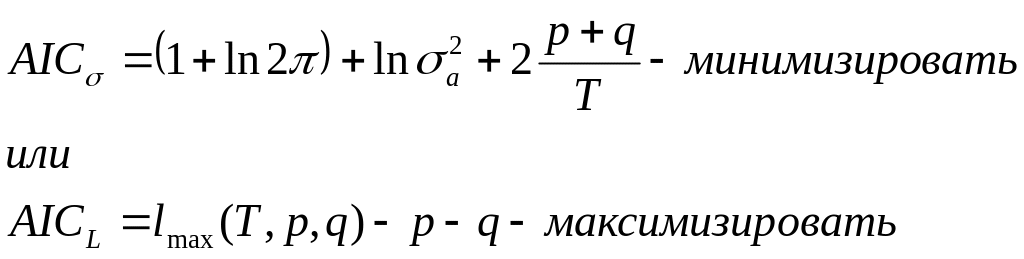
где a2—
дисперсия ошибок; lmax(T,p,q)
— логарифмическая функция правдоподобия
модели ARMA с коэф-ами р и q соотв-но. Кр.
Шварца:
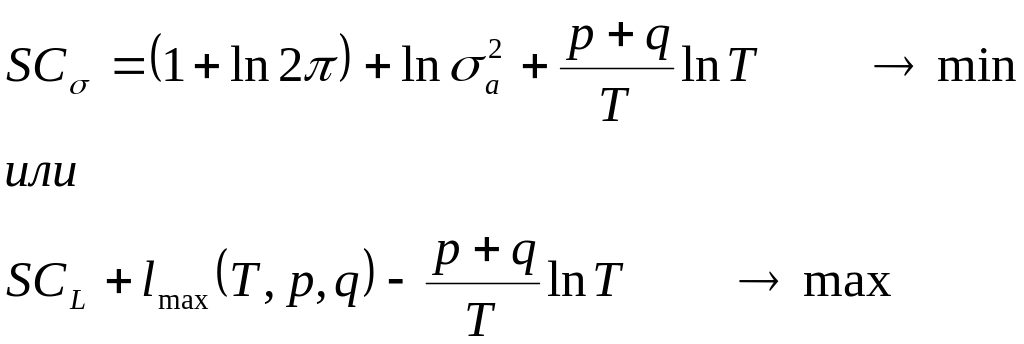
48.Общая хар-ка моделей с распределенным лагом и моделей авторегрессии. Интерпретация пар-ов моделей с распределенным лагом и моделей авторегрессии.
М. выделить два
основных типа динамических эконометрических
моделей: 1)модели авторегрессии; 2)модели
с распределенным лагом. Для этих моделей
знач-ия переменной за прошлые периоды
времени непосредственно включены в
модель. В эти модели включены переменные,
хар-ющие ожидаемый или желаемый уровень
рез-та, или один из факторов в момент
времени t. При исследовании экономических
процессов нередко приходится моделировать
ситуации, когда значение результативного
признака yt
в текущий момент времени t формируется
под воздействием ряда факторов t–1,
t-2,..., t–l.
Эконометрическое моделирование
осуществляется с применением моделей,
содержащих не только текущие, но и
лаговые значения факторных переменных.
Эти модели наз моделями
с распределенным лагом.
Прим:![]() .
Наряду с лаговыми знач-ями незав-ых
переменных на вел-ну зависимой переменной
текущего периода могут оказывать влияние
ее значения в прошлые моменты времени.
Эти процессы обычно описывают с помощью
моделей с
авторегрессией:
.
Наряду с лаговыми знач-ями незав-ых
переменных на вел-ну зависимой переменной
текущего периода могут оказывать влияние
ее значения в прошлые моменты времени.
Эти процессы обычно описывают с помощью
моделей с
авторегрессией:
![]() .
Интерпретация
пар-ов моделей с распределенным лагом
и моделей авторегрессии. Рассмотрим
модель с распр лагом в ее общем виде в
предположении, что максимальная величина
лага конечна и равна l:
.
Интерпретация
пар-ов моделей с распределенным лагом
и моделей авторегрессии. Рассмотрим
модель с распр лагом в ее общем виде в
предположении, что максимальная величина
лага конечна и равна l:
![]() Данная модель говорит о том, что если в
некоторый момент времени t происходит
изменение незав-ой переменной х, то это
изменение будет влиять на значения
переменной у в течение p следующих
моментов времени. Коэф-т регрессии b0
хар-ет среднее абсолютное изменение yt
при изменении xt
на одну единицу в данный фиксированный
момент t, поэтому его наз краткосрочным
мультипликатором.
Введем обозначения βj
= bj
/ b,
j=0,1,2…
βj
– относительные
коэф-ты модели с распр лагом.
Для любого у
0 < βj
<1 и ∑
βj=1.
В этом случае j
явл весами
для соотв-щих коэф-ов bj.Используя
j
можно определить дополнит хар-ки:
1)вел-ну среднего лага:
Данная модель говорит о том, что если в
некоторый момент времени t происходит
изменение незав-ой переменной х, то это
изменение будет влиять на значения
переменной у в течение p следующих
моментов времени. Коэф-т регрессии b0
хар-ет среднее абсолютное изменение yt
при изменении xt
на одну единицу в данный фиксированный
момент t, поэтому его наз краткосрочным
мультипликатором.
Введем обозначения βj
= bj
/ b,
j=0,1,2…
βj
– относительные
коэф-ты модели с распр лагом.
Для любого у
0 < βj
<1 и ∑
βj=1.
В этом случае j
явл весами
для соотв-щих коэф-ов bj.Используя
j
можно определить дополнит хар-ки:
1)вел-ну среднего лага:![]() и
представляет собой средний период, в
теч кот-ого будет происходить изменение
рез-та под воздействием изменения
фактора в момент времени t. 2)Медианного
лага — это вел-на лага lMe,
для кот ∑ βj≈0,5.
Это период времени, в теч кот с момента
времени t будет реализована половина
общего воздействия фактора на рез-т.
и
представляет собой средний период, в
теч кот-ого будет происходить изменение
рез-та под воздействием изменения
фактора в момент времени t. 2)Медианного
лага — это вел-на лага lMe,
для кот ∑ βj≈0,5.
Это период времени, в теч кот с момента
времени t будет реализована половина
общего воздействия фактора на рез-т.
Обратимся теперь
к модели авторегрессии:
![]() .
Вел-на bo
хар-ет краткосрочное изменение yt
под воздействием изменения xt
на 1 ед. Общие абсолютные изменения
рез-та в момент t+1 составит b0с1
единиц, в (t+2) – b0с12
ед и т.д. След-но b
= b0
+ b0
cl
+ b0
cl2
+ b0
сl3+...
Для реализации стабильности ур-ия yt
очевидно необх-мо |с1|<1.
Тогда учитывая св-во суммы бескон геом
прогрессии получим b=b0/(1-c1).
Данная интерпитация предполагает
наличие бесконечного лага.
.
Вел-на bo
хар-ет краткосрочное изменение yt
под воздействием изменения xt
на 1 ед. Общие абсолютные изменения
рез-та в момент t+1 составит b0с1
единиц, в (t+2) – b0с12
ед и т.д. След-но b
= b0
+ b0
cl
+ b0
cl2
+ b0
сl3+...
Для реализации стабильности ур-ия yt
очевидно необх-мо |с1|<1.
Тогда учитывая св-во суммы бескон геом
прогрессии получим b=b0/(1-c1).
Данная интерпитация предполагает
наличие бесконечного лага.
