43. Нестационарные временные ряды. Метод разностей и интегрируемость.

Реальные временные ряды, харак-щие экон-ие процессы, как правило не стационарны. Обычно эти ВР содержат тренд (возраст-щий, убыв) илиимеют колебания на фоне общего тренда. Также возможно наличие гетероскедастичности и изменяющейся автокорреляции. Ряд нестационарен, если среднее или дисперсия данного ряда изменяются во времени, а также если ковариация зависит от конкретных моментов времени ее изменения.. Типичные примеры ВР: ставка обменных курсов индустриально развитых стран, напр, доллора и йеней, показатели ВВП и тд. Для реальных эконом. процессов осн причиной, вызывающей нестационарность ВР, является высокая инерционность внезапного воздействия (шока) на ВР. Во время эконом-ого спада или бума основные макроэконом-ие показатели имеют сильные изменения и остаются на новом уровне в течение длительного промежутка времени, не возвращаясь к своему прежнему положению. Для получения критерия, который м.б. бы использовать для выявления нестационарности рядов, рассмотрим авторегрессионный процесс Y_t первого порядка: Y_t=α ₀+α ₁Y_t-1+ε _t. Между стац и нестац ВР имеется существенное отличие – единовременное шоковое воздействие на стацион-ый ряд носит временный хар-ер. Со временем эффект рассеивается, и значения временного ряда возвращаются к своему долгосрочному среднему значению. След-но, долгосрочный прогноз стационарного ряда сходится к безусловному среднему. Для облегчения идентификации стационарных рядов будем использовать след св-ва: 1.Уровни ряда колеблются вокруг постоянного долгосрочного среднего значения. 2.Временной ряд имеет постоянную, не зависящую от времени дисперсию. 3.Временной ряд имеет теоретическую коррелограмму, которая убывает при возрастании длины лага. Метод разностей и интегрируемость. Большинство экон-их ВР нестационарны, но многие методы и модели основаны на предположении о стационарности ВР. Во многих случаях взятие разностей временных рядов позволяет получить стационарные ВР. Т.е. вместо знач-ия ур-ни Х1, Х2, …, Хn рассм их разность: ΔХ1=Х2-Х1, ΔХ2=Х3-Х2 и тд. Первые разности стохастического процесса имеют вид: (1-L)X_t=ΔX_t=X_t - X_t-1. Или для сезонного процесса с длиной периода s: (1-L^s)X_t=Δ_sX_t=X_t - X_t-s Если первые разности ряда x_t стационарны, то ряд x_t называется интегрируемым первого порядка. В противном случае дальнейшее взятие разностей приведет ко вторым разностям: (1-L)²X_t=Δ²X_t =ΔX_t - ΔX_t-1. Если этот ряд стационарен, то ряд x_t называется интегрируемым второго порядка. Если мы получаем первый стационарный ряд после k-кратного взятия разностей, процесс называется интегрируемым к-го порядка.

44. Оценка порядка интегрируемости. Тесты на единичный корень. Интеграционная статистика Дарбина-Уотсона

И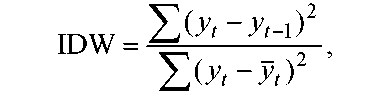 нтеграционная статистика Дарбина-Уотсона явл наиболее простым способом проверки на стационарность ВР Интегр статистика Д-У (IDW) разработана для авторегрессии первого пор Y_t=α₁Y_t-1+ε _t.(1). Данная статистика имеет след вид:

где y_t —ВР, являющийся реализацией процесса Y_t; — выборочная средняя по данному ВР. Если временной ряд у_t — нестационарный, т.е. в уравнении (1) α₁=1, то в числителе получим Σ(y_t-y_t-1)²=Σ ε _t². Для нестационарного ряда это отношение будет близко к 0. Можно сказать, что процесс у_t — не стационарный, если IDW≈0, и у_t — стационарный, если IDW≈2. Зам: Утверждение о стационарности процесса не требует подтверждения рез-тами других тестов, однако нестационарность ставит задачу определения порядка интегрируемости либо заключения о том, что процесс неинтегрируем вообще. Обычно не известно заранее, какие компоненты содержит ВР, включает ли он свободный член или тренд. Поэтому использование интеграционной статистики Д-У на этапе оценки интегрируемости ВР без применения дополн-ых тестов может привести к ошибочным выводам. Для оценки стационарности или порядка интегрируемости данных ВР необх-мо сопоставить расчетные значения IDW-статистики с критическими. Зам. Поскольку распределение IDW-статистики не соответствует ни одному из известных теоретических распределений, критические значения будут представлены не единичными значениями, а отрезком. Критические значения применяются для проверки гипотезы Н₀ : IDW=2 (процесс стац-ный) и альтернативной ей гипотезы Н₁ : IDW≠2 (процесс не явл стац-ным). А также гипотезы H*₀ : IDW=0 (процесс нестац-ный) и альтернативной гипотезы H*₁ IDW≠ 0 (процесс не явл нестац-ным).