
- •11. Оценка дисперсии ошибок.
- •12. Оценка существенности параметров линейной регрессии и корреляции
- •13. Интервалы прогноза по линейному уравнению регрессии
- •14. Нелинейная регрессия. Линеаризируемые и нелинеаризируемые модели.Эластичность
- •15. Корреляция для нелинейной регрессии. Средняя ошибка аппроксимации.
- •16. Множественная регрессия. Спецификация модели. Отбор факторов.
- •17. Мнк для множественной регрессии. Мультиколлинеарность ее последствия.
- •19. Множественная корреляция. Скорректированный индекс детерминации.
- •20. Частная корреляция при множественной регрессии. Прцедура пошагового отбора переменных
16. Множественная регрессия. Спецификация модели. Отбор факторов.
Парная регрессия справедлива тогда, когда имеется 1 знач. фактор влияющий на рез-т. Если знач. явл. несколько факторов исполь-ся модель множественной регрессии.
Пусть на фактор у оказывает влияние несколько значимых факторов (регрессоров) х1,…,хn ур-ние множ. регрессии:
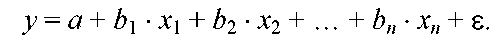
где bj — частные коэ-ты регрессии по j-ому фактору j=1,n .
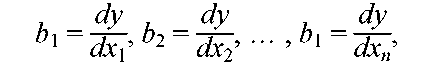
Указывает на сколько ед. в ср. изменится рез-т при изменении соот-его регрессора на 1, при условии что остальные регрессоры не изменяются.
Спецификация
Построение ур-ния множ. регрессии начинается с реш. вопроса о спецификации модели, кот. вкл. в себя 2 осн. вопроса: отбор факторов и выбор вида уравнения регрессии.
Отбор факторов при построении множественной регрессии
Включение в ур-ние множ. регрессии того или иного набора факторов связано, прежде всего, с представлением исследователя о природе взаимосвязи моделируемого показателя с др. эконом. явлениями. Факторы, вкл-ые во множ. регрессию, должны отвечать следующим требованиям:
они д.б. кол-но измеримы. Если в регрессию включен качественный хар-рему придают кол-ую опред-ть. Если нет возможности ранжировать использ. Фиктивные переменные.
2.они
не должны быть интеркоррелированы и
тем более находиться в точной
функциональной связ, т.е. если вкл.
факторы с высокой интеркорреляцией,
когда Ryx1<Rх1х2
для
зависимости у=а+b1х1+b2х2+ε
может
привести к нежелательным
последствиям — система ур-ний будет
обусловленной, что влечет неустойчивость
и ненадежность оценок. Если
между факторами существует высокая
корреляция, то нельзя определить
их изолированное влияние на результативный
показатель и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в
уравнении
![]() предполагается,
что факторы
предполагается,
что факторы
![]() и
и
![]() независимы
друг от друга, т. е.
независимы
друг от друга, т. е.
![]() .
Тогда можно говорить, что параметр
.
Тогда можно говорить, что параметр
![]() измеряет
силу влияния фактора
на
результат
измеряет
силу влияния фактора
на
результат
![]() при неизменном
значении фактора
.
Если же
при неизменном
значении фактора
.
Если же
![]() ,
то с изменением
фактора
фактор
не
может оставаться неизменным. Отсюда
,
и
,
то с изменением
фактора
фактор
не
может оставаться неизменным. Отсюда
,
и
![]() нельзя
интерпретировать как показатели
раздельного влияния
и
на
.
Включаемые
во множественную регрессию факторы
должны объяснить вариацию
независимой переменной. Если строится
модель с набором
нельзя
интерпретировать как показатели
раздельного влияния
и
на
.
Включаемые
во множественную регрессию факторы
должны объяснить вариацию
независимой переменной. Если строится
модель с набором
![]() факторов,
то для нее рассчитывается показатель
детерминации
факторов,
то для нее рассчитывается показатель
детерминации
![]() ,
который фиксирует
долю объясненной вариации результативного
признака за счет рассматриваемых в
регрессии
факторов.
Влияние других не учтенных в модели
факторов
оценивается как
,
который фиксирует
долю объясненной вариации результативного
признака за счет рассматриваемых в
регрессии
факторов.
Влияние других не учтенных в модели
факторов
оценивается как
![]() с
соответствующей остаточной дисперсией
с
соответствующей остаточной дисперсией
![]() .
При
дополнительном
включении в регрессию
.
При
дополнительном
включении в регрессию
![]() фактора коэффициент детерминации должен
возрастать, а остаточная дисперсия
уменьшаться:
фактора коэффициент детерминации должен
возрастать, а остаточная дисперсия
уменьшаться:
![]() ,
а
,
а
![]() .
.
Если
же этого не происходит и данные показатели
практически мало отличаются друг от
друга, то включаемый в анализ фактор
![]() не
улучшает модель и
практически является лишним фактором.
Так, если для регрессии, включающей пять
факторов, коэффициент детерминации
составил 0,857 и включение шестого фактора
дало коэффициент детерминации 0,858, то
вряд ли целесообразно дополнительно
включать в модель этот фактор.
не
улучшает модель и
практически является лишним фактором.
Так, если для регрессии, включающей пять
факторов, коэффициент детерминации
составил 0,857 и включение шестого фактора
дало коэффициент детерминации 0,858, то
вряд ли целесообразно дополнительно
включать в модель этот фактор.
