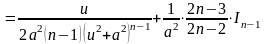- •Зразки розв’язування задач.
- •4. Рівняння площини у відрізках на осях
- •3.5. Пряма в просторі
- •3.5.1. Рівняння прямої в просторі
- •3.5.2. Кут між двома прямими в просторі. Умови паралельності та перпендикулярності
- •3.5.3. Кут між прямою і площиною. Умови паралельності та перпендикулярності прямої і площини
- •24.Функція,способи задання,область визначення та область значень.Елементарні функції та її графіки.
- •Означення показникової функції.
- •Задачі, які приводять до поняття показникової функції.
- •3. Побудова графіка показникової функції.
- •Властивості показникової функції.
- •Перетворення графіків функцій
- •Зразки розв’язування задач
- •Інтегрування раціональних дробів
Інтегрування раціональних дробів
Відношення
 двох многочленів
двох многочленів
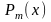 і
і
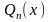 відповідно m-го
і n-го
степеня називається дробно-раціональною
функцією або раціональним дробом.
відповідно m-го
і n-го
степеня називається дробно-раціональною
функцією або раціональним дробом.
Раціональний
дріб називається правильним, якщо
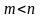 .
Якщо ж
.
Якщо ж
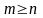 ,
то раціональний дріб називається
неправильним. В цьому випадку розділивши
на
одержимо:
,
то раціональний дріб називається
неправильним. В цьому випадку розділивши
на
одержимо:
|
(1.10) |
де
 і
і
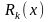 -
многочлени відповідно m-n-го
та k-
го степенів, причому
-
многочлени відповідно m-n-го
та k-
го степенів, причому
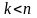 ,
тобто дріб
,
тобто дріб
 - правильний.
- правильний.
Знаменник розкладається на добуток лінійних і квадратних множників, перші з яких лінійні відповідають дійсним кореням , а другі (квадратні) – комплексно спряженим кореням . Кратні корені характеризуються відповідними степенями цих множників.
Елементарними раціональними дробами називаються такі правильні раціональні дроби.
а)
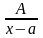 ;
б)
;
б)
 ;
;
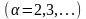 ;
в)
;
в)
 ;
г)
;
г)

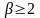 ;
;
де
А, а,
М, N, p, q –
дійсні числа, а тричлен
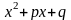 не має дійсних коренів.
не має дійсних коренів.
Отже,
правильний раціональний дріб, у якого
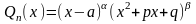 тобто
має дійсний корінь кратності
і два комплексно спряжені корені
кратності
тобто
має дійсний корінь кратності
і два комплексно спряжені корені
кратності
 ,
розкладається на суму елементарних
дробів так:
,
розкладається на суму елементарних
дробів так:
|
(1.11) |
Якщо має більше дійсних і комплексно-спряжених коренів, то розклад (1.11) відповідно розширюється.
Нехай потрібно знайти інтеграл
|
(1.12) |
Згідно з (1.10) інтеграл виду (1.12) запишеться так
|
(1.13) |
Інтеграл від многочлена обчислюється за табличним інтегралом 1, а інтеграл від правильного дробу, згідно з (1.11) зводиться до обчислення інтегралів від елементарних раціональних дробів.
Розглянемо ці інтеграли. Скористаємось наведеними вище перетвореннями диференціала і табличними інтегралами 2 і 1. Тоді для елементарних дробів а) і б) будемо мати:
І.
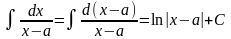 ;
;
ІІ.
 ;
;
ІІІ. Обчислення інтеграла від елементарного дробу в) базується на виділенні у знаменнику дробу ( в квадратному тричлені) повного квадрату, тобто

В результаті одержимо:
|
(1.14) |
Далі
можливі такі випадки: якщо т=0,
тоді при
 інтеграл зводиться до інтегралу 11, а
при
інтеграл зводиться до інтегралу 11, а
при
 - до інтегралу 12. Якщо ж
- до інтегралу 12. Якщо ж
 ,
тоді інтеграл (1.14) зводиться до інтегралів
13 і 11, або до інтегралів 13 і 12. Як це
робиться , покажемо на конкретних
прикладах.
,
тоді інтеграл (1.14) зводиться до інтегралів
13 і 11, або до інтегралів 13 і 12. Як це
робиться , покажемо на конкретних
прикладах.
Приклад 1.
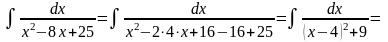

Приклад 2.
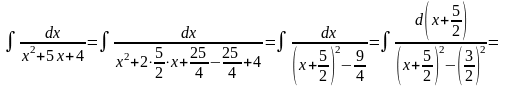
 ;
;
Приклад 3.
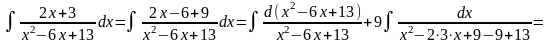
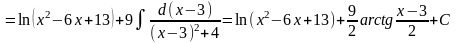
Приклад 4.
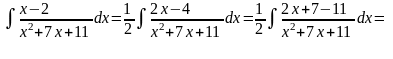

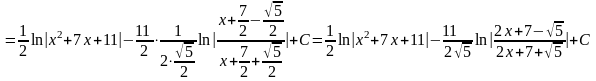
Зауваження. Перетворення, які були зроблені у чисельниках прикладів 3, 4 пов’язані із виділенням у них похідних або диференціалів знаменників та зведенням їх до інтеграла 13.
IV. Інтеграл виду:
 де
де

підстановкою
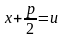 зводиться до суми двох інтегралів
зводиться до суми двох інтегралів
 ,
де
,
де
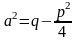 ;
;
Перший із цих інтегралів обчислюється згідно з інтегралом 1, а другий за рекурентною формулою.
|
(1.15) |
Приклад.
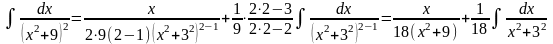 =
=
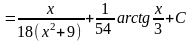 .
.
Питання інтегрування неправильного раціонального дробу розглянемо на такому прикладі:
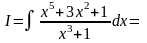 Виділимо
цілу частину дробу
Виділимо
цілу частину дробу
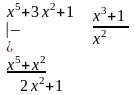
= .
.
Розкладемо
правильний дріб на елементарні і зведемо
вираз до спільного знаменника.
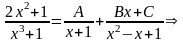
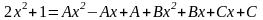 .
.
Прирівняємо коефіцієнти при невідомих і розв’яжемо систему рівнянь.

В результаті:


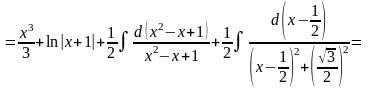
=

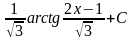 .
.
46.Інтегрування ірраціональних функцій
Функція
 називається раціональною від змінних
називається раціональною від змінних
 ,
якщо над цими змінними і дійсними
числами виконується скінчене число
операцій додавання, віднімання, множення
і ділення. Змінні
можуть бути і функціями. Наприклад,
функція
,
якщо над цими змінними і дійсними
числами виконується скінчене число
операцій додавання, віднімання, множення
і ділення. Змінні
можуть бути і функціями. Наприклад,
функція
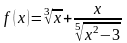 є раціональною функцією відносно функції
є раціональною функцією відносно функції

 ,
тобто
,
тобто
 .
.
Розглянемо способи інтегрування таких функцій.
Інтеграл
 раціоналізується підстановкою
раціоналізується підстановкою
 .
.
Звідси
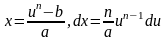 .
Отже
.
Отже
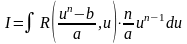
Приклад. Знайти інтеграл.

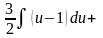
 =
=
=
Інтеграл більш загального виду
 раціоналізується
підстановкою
раціоналізується
підстановкою
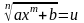 .
.
Звідси
 ,
,
 ,
або
,
або
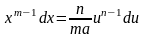 .
Отже
.
Отже
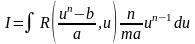 .
.
Приклад. Знайти інтеграл.

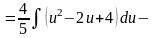

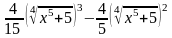 +
+
 .
.
Інтеграл виду
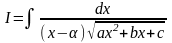 знаходиться підстановкою
знаходиться підстановкою
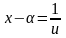 ,
,
 ;
;
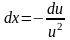 .
В залежності від значень a,b,c,
він
зводиться до одного із табличних
інтегралів 9 або 10.
.
В залежності від значень a,b,c,
він
зводиться до одного із табличних
інтегралів 9 або 10.
Приклад. Знайти інтеграл.

=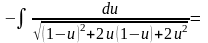

=
47.Інтегрування тригонометричних функцій
Важливе значення у прикладних питаннях деяких природничих наук мають інтеграли.
|
(1.16) |
де m і n цілі невід’ємні числа.
Тут можливі такі випадки:
а)
хоча б один із показників m
або
n
непарне число. В цьому випадку інтеграл
(1.16) знаходиться підстановкою
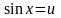 ,
якщо n-непарне,
і підстановкою
,
якщо n-непарне,
і підстановкою
 ,
якщо m-непарне.
Якщо ж m
і
n
обидва непарні, то можна брати будь-яку
з цих підстановок.
,
якщо m-непарне.
Якщо ж m
і
n
обидва непарні, то можна брати будь-яку
з цих підстановок.
Приклад. Знайти інтеграл.
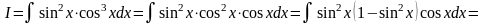
 =
= .
.
б) обидва показники m і n парні числа. В цьому випадку інтеграл (1.16) береться за допомогою тригонометричних тотожностей пониження степеня, а саме, формул подвійного аргументу:
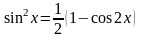 ,
,
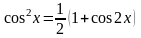 ,
,

Приклад. Знайти інтеграл.
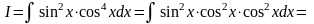
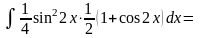

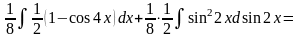
 .
.
В теорії рядів Фур’є важливу роль відіграють інтеграли виду:
|
(1.17) |
Всі ці інтеграли обчислюються на основі наступних тригонометричних формул:
 ,
,

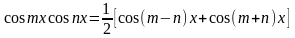 .
.
Приклад. Знайти інтеграл.
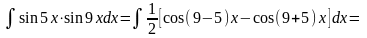
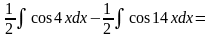
 .
.
48.Диференціальні рівняння основні поняття та означення.
Рішення різних геометричних, фізичних і інженерних задач часто приводять до рівнянь, які зв'язують незалежні змінні, з будь-якою функцією цих змінних і похідними цієї функції різних порядків.
Як приклад можна розглянути найпростіший випадок рівноприскоренного руху матеріальної точки.
Відомо, що переміщення матеріальної точки рівноприскоренного руху є функцією часу і виражається формулою:
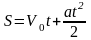 .
.
У свою чергу прискорення a є похідною за часом t від швидкості V , що також є похідною за часом t від переміщення S . Тобто
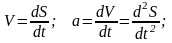
Тоді
одержуємо:
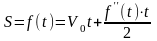 − рівняння зв'язує функцію f(t) з незалежною
змінною t
і похідною другого порядку функції
f(t).
− рівняння зв'язує функцію f(t) з незалежною
змінною t
і похідною другого порядку функції
f(t).
Визначення. Диференціальним рівнянням називається рівняння, що зв'язує незалежні змінні, їхні функції і похідні (або диференціали) цієї функції.
Визначення. Якщо диференціальне рівняння має одну незалежну змінну, то воно називається звичайним диференціальним рівнянням.
Це означення в загальному вигляді математично можна записати так
F( х, у, у', у'', ..., уⁿ ) = 0. якщо ж незалежних змінних дві або більше, то таке диференціальне рівняння нази-вається диференціальним рівнянням у частинних похідних.
Приклад.
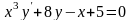 − звичайне
диференціальне рівняння 1 – го порядку.
− звичайне
диференціальне рівняння 1 – го порядку.
У
загальному виді записується
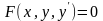 .
.
 − звичайне
диференціальне рівняння 2 – го порядку.
− звичайне
диференціальне рівняння 2 – го порядку.
У
загальному виді записується
 .
.
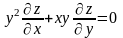 − диференціальне
рівняння в частинних похідних першого
порядку.
− диференціальне
рівняння в частинних похідних першого
порядку.
Визначення. Найвищий порядок похідної, що містить диференціальне рівня-ння, називають порядком диференціального рівняння.
Наприклад:
рівняння ху' – 3у'' = 2cos x – другого порядку;
рівняння у''' – х² у' = 0 – третього порядку.
Визначення. Загальним розв'язком диференціального рівняння n – го поряд-ку називають функцію у, яка залежить від аргументу х та n довільних сталих С1, С2, ... , Сn, тобто має вигляд
у = q ( x, C1, C2, … , Cn ),
яка, при її підстановці в рівняння, перетворює рівняння в тотожність.
Найчастіше сталі С1, С2, ... , Сn обирають не довільно, а так, щоб розв'язок рівняння задовольняв деяким початковим умовам. Для знаходження n довіль-них сталих треба задати n початкових умов.
Процес знаходження розв'язків диференціального рівняння називають інте-груванням диференціального рівняння.
Визначення. Диференціальним рівнянням першого порядку називається рів-няння виду
F( х, у, у' ) = 0 або у' = f (х, у),
яке пов’язує незалежну змінну х, невідому функцію у = у( х ) та її похідну.
Визначення. Розв’язком диференціального рівняння на деякому інтервалі
(a;b) називається диференційована на цьому інтервалі функція у = q ( x ), яка при підстановці в рівняння
F( x, у, у' ) = 0
перетворює його в тотожність по х на (a;b).
Функція у = q (x, C ), яка залежить від аргументу і довільної сталої C, називається загальним розв'язком рівняння в області D, якщо вона задовольняє дві умови:
функція q ( x, C ) є розв'язком рівняння при будь- якому значенні сталої C із деякої множини;
для довільної точки ( х0 , у0 ) D можна знайти таке значення C = C0, що функція у = q ( x, C0 ) задовольняє початкову умову q ( x0, C0 ) = у0.
Визначення . Частинним розв'язком рівняння називається функція
у = q ( x, C0 ),
яка утворюється із загального розв’язку у = q ( x, C ) при певному значенні сталої C= C0 .
Якщо загальний розв'язок диференціального рівняння знайдено в неявному вигляді, тобто у вигляді рівняння
Ф ( х, у, С) = 0,
то такий розв'язок називають загальним інтегралом диференціального рівнян-ня
F ( x, у, у' ) = 0.
Рівність Ф ( х, у, С0 ) = 0 називають частинним інтегралом рівняння.
Найвищій порядок похідної, яка входити в диференціальне рівняння, нази-вається порядком диференціального рівняння.
Задача Коші
Визначення. Сумісне завдання диференціального рівняння та відповідної кількості початкових умов називають задачею Коші.
Задача в якій необхідно знайти частинний розв'язок рівняння у' = f ( x, у) при початковій умові у ( х0 ) =у0, називається задачею Коші для диференціаль-ного рівняння першого степеня.
У дослідженнях різноманітних життєвих та економічних проблем найчастіше використовують диференціальні рівняння першого та другого порядків певних типів та відповідні їм задачі Коші.
У теорії звичайних диференціальних рівнянь можна виділити дві основні
задачі:
знаходження диференціального рівняння та початкових умов, які описують ситуацію або процес, який досліджують;
розв'язування заданої задачі Коші або знаходження загального розв'язку заданого диференціального рівняння.
Приклад.
Знайти
загальне рішення диференціального
рівняння
 .
.
Розв’язування.
Загальне рішення диференціального рівняння знаходиться за допомогою інтегрування лівої і правої частин рівняння, що попередньо перетворено, таким чином:



Тепер
інтегруємо:


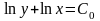
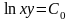

 − це
загальне рішення даного диференціального
рівняння.
− це
загальне рішення даного диференціального
рівняння.
Припустимо, задані деякі початкові умови: x0 = 1; y0 = 2, тоді маємо

При підстановці отриманого значення постійної в загальне рішення одержуємо частинний розв’язок при заданих початкових умовах (рішення задачі Коші)
 .
.
Приклад.
Знайти
загальне рішення диференціального
рівняння:
 Знайти особливе рішення, якщо воно
існує.
Знайти особливе рішення, якщо воно
існує.



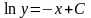
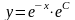
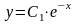 .
.
Дане диференціальне рівняння має також особливе рішення у = 0. Це рішення неможливо одержати із загального, однак при підстановці у вихідне рівняння одержуємо тотожність. Думка, що рішення y = 0 можна одержати із загального рішення при С1 = 0 помилкова, адже C1 = e 0.