Глава 1 Параметрические регрессионные модели

Глава посвящена параметрическим регрессионным моделям. Дается представление о линейной парной и множественной регрессии, приводятся сведения о методе наименьших квадратов (МНК) и вывод критерия наименьших квадратов. Рассматривается линейный метод наименьших квадратов в матричной форме, предлагается вариант МНК с использованием ортогональных полиномов, выводится рекуррентная форма линейного МНК. Далее метод МНК распространяется на нелинейный случай с применением метода линеаризации. Кратко описываются другие методы построения статических моделей – методы максимального правдоподобия и максимума апостериорной вероятности. В заключение представлен адаптивный подход к идентификации, реализованный с использованием метода стохастической аппроксимации.

1.1. Линейная регрессия

Взаимосвязь между случайными величинами может быть представлена разными способами. Например, эту связь можно описать с помощью различных коэффициентов корреляции (линейных, частных, корреляционного отношения и т. п.). В то же время эту связь можно выразить и как зависимость между аргументом (величиной) X и функцией Y. В этом случае задача будет состоять в нахождении зависимости вида или, напротив, в нахождении зависимости вида . Зависимость между случайными величинами, выраженная функционально, называется регрессией.

Графическое выражение регрессионного уравнения называют линией ре- грессии. Линия регрессии выражает наилучшее предсказание зависимой переменной Y по независимым переменным X. Эти независимые переменные, а их может быть много, носят название предикторов.

Регрессию выражают с помощью двух уравнений регрессии, которые в самом простом случае являются линейными:

,	(1.1)
.	(1.2)

В уравнении (1.1) Y – зависимая переменная, Х – независимая переменная, – свободный член, – коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат. В уравнении (1.2) Х – зависимая переменная, Y – независимая переменная, – свободный член, – коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат (рис. 1.1).

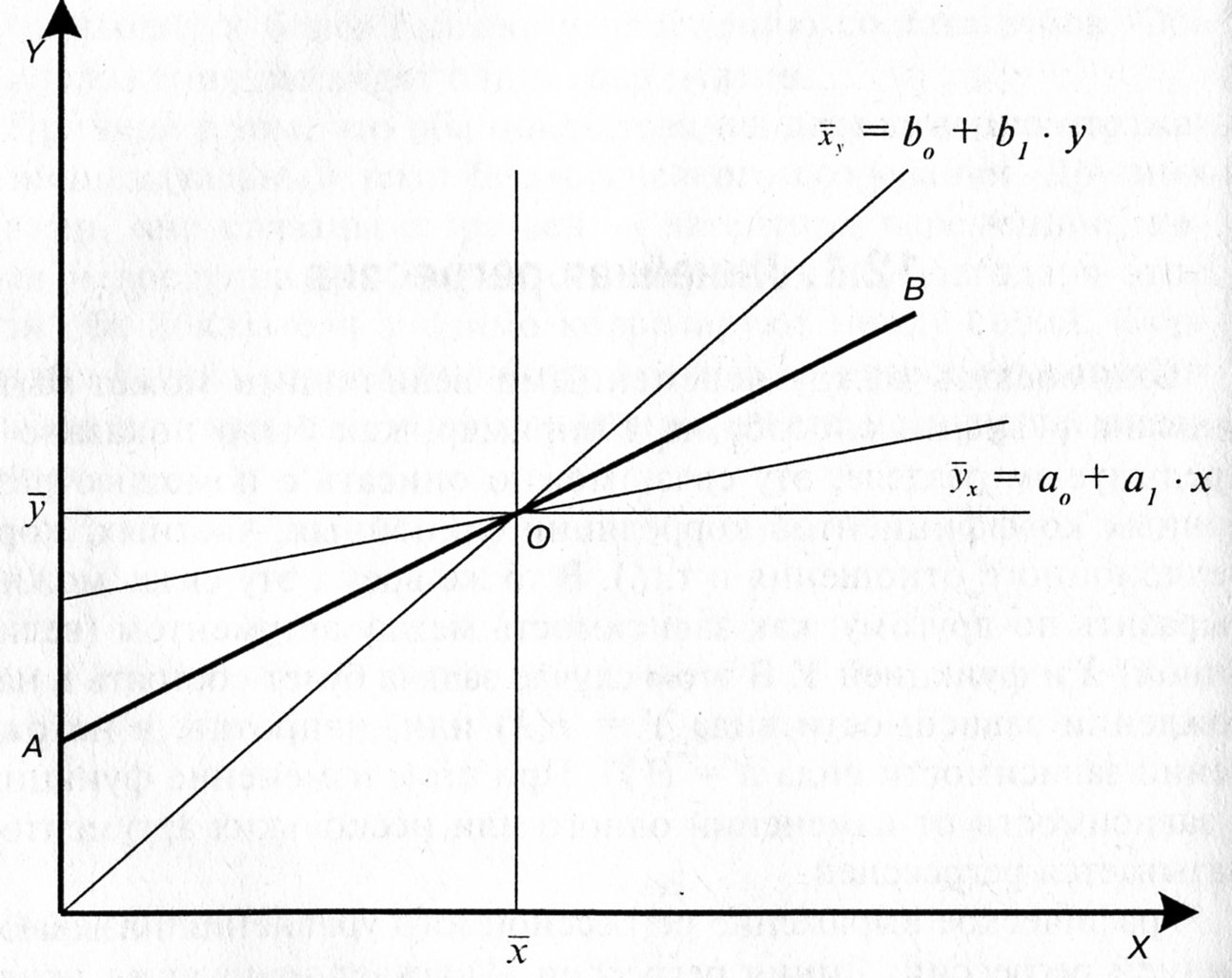
Рис. 1.1. Линии регрессии Х по Y и Y по X

Линии регрессии пересекаются в точке с координатами, соответствующими средним арифметическим значениям корреляционно связанных между собой переменных Х и Y. Линия АВ, проходящая через точку О, соответствует линейной функциональной зависимости между переменными величинами Х и Y, когда коэффициент корреляции между Х и Y равен 1. При этом наблюдается такая закономерность: чем сильнее связь между Х и Y, тем ближе обе линии регрессии к прямой АВ, и, наоборот, чем слабее связь между этими величинами, тем больше линии регрессии отклоняются от прямой АВ. При отсутствии связи между Х и Y линии регрессии оказываются под прямым углом по отношению друг к другу и в этом случае .

Количественное представление связи (зависимости) между Х и Y (между Y и X) называется регрессионным анализом. Главная задача регрессионного анализа заключается в нахождении коэффициентов , , и . При этом коэффициенты регрессии и показывают, насколько в среднем величина одной переменной изменяется при изменении на единицу меры другой.

Коэффициент регрессии в уравнении (1.1) можно подсчитать по формуле

(1.3)

а коэффициент в уравнении (1.2) – по формуле

,

(1.4)

где – коэффициент корреляции между переменными Х и Y; – среднеквадратическое отклонение, подсчитанное для переменной Х:

;

– среднеквадратическое отклонение, подсчитанное для переменной Y:

;

N – количество элементов выборки.

Коэффициенты регрессии также можно вычислить без подсчета среднеквадратических отклонений по формулам

,	(1.5)
.	(1.6)

В случае если коэффициент корреляции неизвестен, коэффициенты регрессии можно определить по следующим формулам:

,	(1.7)
.	(1.8)

Сравнивая формулы (1.7) и (1.8), мы увидим, что в числителе стоит одна и та же величина: . Последнее говорит о том, что величины a₁, b₁ и взаимосвязаны. Более того, зная две из них, всегда можно получить третью. Например, зная величины a₁ и b₁, можно легко получить :

.

(1.9)

Формула (1.9) достаточно очевидна, поскольку, умножив коэффициент а₁, вычисленный по формуле (1.3), на коэффициент b₁, вычисленный по формуле (1.4), получим:

.

Формула (1.9) очень важна, поскольку она позволяет по известным значениям коэффициентов регрессии а₁ и b₁ определить коэффициент корреляции и, кроме того, проверить правильность расчета коэффициента корреляции. Как и коэффициент корреляции, коэффициенты регрессии характеризуют только линейную связь и при положительной связи имеют знак «плюс», при отрицательной – знак «минус».

Свободные члены а₀ и b₀ в уравнениях регрессии можно вычислить по следующим формулам:

,	(1.10)
.	(1.11)

Зависимость между несколькими переменными величинами выражают уравнением множественной регрессии, которая может быть как линейной, так и нелинейной.