Перспектива окружности.

Построение перспективы ок­ружности находит применение при изо­бражении архитектурных сооружений и внутренних пространств зданий круг­лой формы, а также при построении Перспективы сводов, арок и других ар­хитектурных фрагментов.

Проецирующие лучи, проходящие через точку зрения и окружность, обра­зуют наклонный конус с круговым основанием (рис. 291).

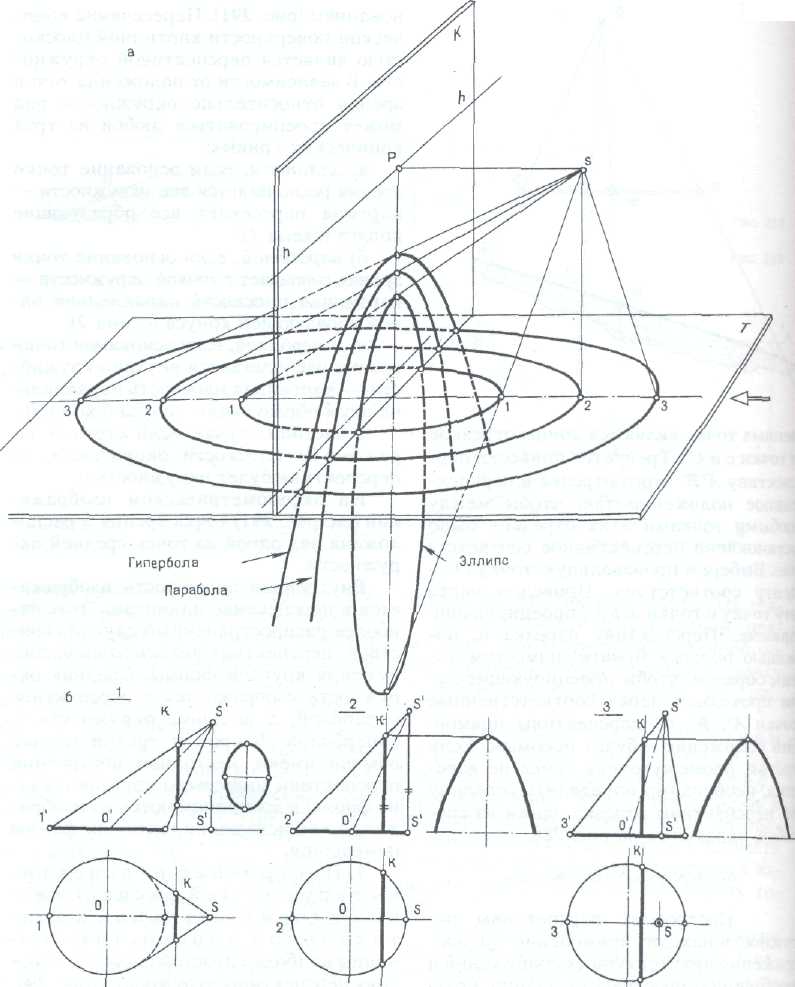
Пересечение кони­ческой поверхности картинной плоско­стью является перспективой окружно­сти. В зависимости от положения точки зрения относительно окружности она может проецироваться любой из трех конических кривых:

• а) эллипсом, если основание точки зрения располагается вне окружности —картина пересекает все образующие конуса (схема /);

• б) параболой, если основание точки зрения совпадает с точкой окружности —картинная плоскость параллельна одной образующей конуса (схема 2);

• в) гиперболой, если основание точки зрения располагается внутри окружности — картинная плоскость параллель­на двум образующим конуса (схема 3).

В частном случае, если картина па­раллельна плоскости окружности, ее перспектива будет окружностью.

На аксонометрическом изображе­нии (см. рис. 291) точка зрения S распо­ложена над одной из точек средней ок­ружности.

Внутренняя окружность изобража­ется в перспективе эллипсом. Этот на­иболее распространенный случай свой­ствен перспективе внешнего вида соо­ружения круглой формы.

Средняя ок­ружность изображается в перспективе параболой, а внешняя окружность — гиперболой.

Второй и третий случаи обычно имеют место при построении перспективы интерьера круглой в пла­не формы и воспринимаются на изобра­жении как искажение истинной формы помещения.

1. Построение перспекти­вы окружностей, расположен­ных в горизонтальной и вер­тикальной плоскостях.

При­меним наиболее простой способ постро­ения перспективы окружности (рис. 292, а) — с помощью построения перспекти­вы описанного квадрата и восьми точек эллипса аналогично построению пада­ющей тени и аксонометрии окружно­сти.

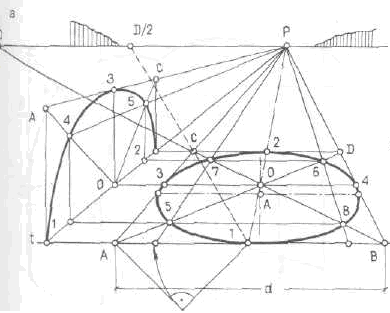
Построим перспективу описанного квадрата, две стороны которого параллельны основанию картины, с по мощью дистанционной точки D.

• Если - дистанционная точка окажется за пре делами чертежа, можно воспользоваться дробной дистанционной точкой D/2,проведя перспективу диагонали полу­квадрата — прямую 1 — D/2 (штриховая линия).

• При вычерчивании кривой эллипса необходимо иметь в виду, чтоточка О — перспектива центра окруж­ности и точка А — центр эллипса не совпадают.

• Аналогично строится перс­пектива вертикальной окружности.

Если необходимо вписать эллипс в уже построенную перспективу квадра­та, стороны которого не параллельны картине (рис. 292, б):

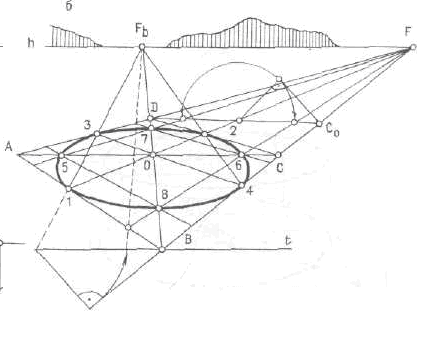
• следует половину стороны квадрата вынести в плоскость картины с помощью любой точки на горизонте и построить на ней равнобед­ренный прямоугольный треугольник с соотношением 0,707 для определения точек эллипса на диагоналях перспек­тивы квадрата.

• Это построение можно выполнить и на горизонтальной прямой DC₀ способом пропорционального деле­ния в перспективе (см. рис. 289, а).

2. Деление перспективы окружности на равные части (рис. 293).

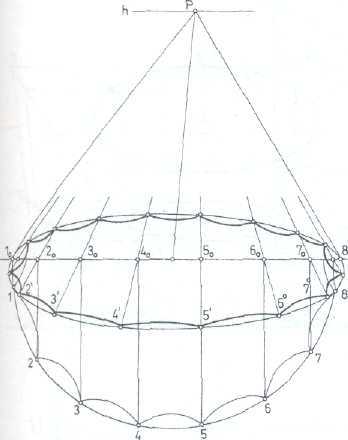
• На фронтальном диаметре перспективы окружности строим полу­окружность, разделенную на части.

• Полученные точки деления переносим вертикальными линиями на перспекти­ву диаметра окружности.

• Эти прямые в перспективе будут перпендикулярны картине, поэтому через точки на диа­метре проводим перспективу прямых, идущих в главную точку Р.

• В пересече­нии с эллипсом получим искомые точки.

Построение перспективы соосных окружностей.

Изображение нескольких окружностей равного или разных диа­метров, расположенных в параллель­ных плоскостях, довольно часто прихо­дится выполнять при построении перс­пективы архитектурных фрагментов и сооружений круглой формы. При этом на основе уже выполненной перспекти­вы одной окружности можно построить перспективы остальных, используя структурное соответствие между ними.