2. Построение перспективы вертикальных плоскостей
— четырех попарно параллельных плоскостей равной высоты (рис. 286).
Вертикальные прямые, параллельные картине, не имеют точек схода и изображаются в перспективе вертикальными.
Чтобы построить перспективу высот четырехугольников, истинный размер можно нанести только в плоскости картины — в точке a, где вертикальный отрезок совмещен с картиной, или найти картинный след 20 — 2 одной из вертикальных плоскостей.
Картинным следом плоскости называется линия пересечения плоскости с картиной.
Проведя перспективу горизонтальных прямых через точки А и 2 вертикальных прямых, закончим построение перспективы плоскостей. Полученное изображение аналогично перспективе прямой четырехгранной призмы — параллелепипеда.
Картинными следами вертикальных плоскостей являются вертикальные прямые аА и 202, совмещенные с картиной.
Картинным следом горизонтальной плоскости нижнего основания призмы служит линия основания картины — прямая tt, на которой расположены картинные следы 1o, 2 o и а горизонтальных прямых, лежащих в предметной плоскости.
3. Перспектива плоскости общего положения (рис. 287).
Наклонная грань призмы является плоскостью общего положения. Перспектива этой грани построена на основе перспективы ее горизонтальной проекции.
Точка схода F3 наклонных (восходящих) прямых АВ и CD расположена на одной вертикали с точкой схода F2 вторичных проекций.
Для построения линии схода плоскости общего положения ABCD надо найти две точки схода наклонных прямых данной плоскости.
Такими точками являются точки схода Fl и F3 и любые другие точки схода, например, точка схода F4 диагонали АС грани.
Прямая, проходящая через эти точки, и есть линия схода данной плоскости, т. е. перспектива бесконечно удаленной прямой плоскости.
Чтобы построить картинный след этой плоскости, достаточно найти картинный след N1 одной прямой, принадлежащей плоскости, например перспективы прямой АD и провести через эту точку прямую, параллельную линии схода плоскости.
Прямая N1N2 является картинным следом плоскости.
Линия схода перспективы плоскости параллельна картинному следу данной плоскости. Линиями схода вертикальных граней призмы будут перспективы бесконечно удаленных прямых этих плоскостей — прямая F2 — F3 и вертикальная прямая, проходящая через точку схода F1. Прямая F1N2 является горизонтальным (предметным) следом перспективы плоскости ABCD.
Деление перспективы отрезков прямых.
Построение перспективы объекта обычно состоит из двух этапов:
1) с помощью плана и фасада строят перспективу основных объемов объекта;
2) членения объема и детали строят непосредственно в перспективе на основе приемов перспективного деления отрезков прямых на части, так как большинство деталей на плане не изображается.
Прямые в перспективе можно отнести к двум основным группам — прямые, параллельные и не параллельные картинной плоскости.
Соотношения отрезка прямой линии, параллельной картине и разделенной на равные или пропорциональные части, не изменяются в перспективе.
Рассмотрим способы деления перспективы отрезков прямых, не параллельных картине.
Деление перспектив отрезков прямых на две равные части (рис. 288).
Чтобы разделить перспективу горизонтального отрезка прямой АВ пополам, следует достроить отрезок до перспективы вертикального четырехугольника, а затем через точку пересечения его диагоналей провести вертикаль . Перспективу горизонтального отрезка можно разделить на две равные части тем же приемом, используя в качестве перспективы второй параллельной прямой линию горизонта (рис. 288, б).
Деление перспектив отрезков прямых на равные или пропорциональные част и (рис. 289).
Деление отрезков прямых линий в перспективе на равные или пропорциональные части основано на том, что стороны угла делятся параллельными прямыми на пропорциональные части.
На рис. 289, а показана перспектива горизонтального отрезка AB.
Требуется разделить его перспективу та части, соответствующие делению его ортогональной проекции ab.
Проведем через один из концов отрезка прямую, параллельную линии горизонта, и перенесем на нее деления с ортогональной проекции отрезка.
Через соответственные точки b и В другого конца отрезка проводим прямую до пересечения с лишен горизонта в точке V.
Прямые, проведенные через точки горизонтального отрезка ab и точку V, разделят перспективу отрезка в данном отношении.
На рис. 289, б приведена перспектива наклонного отрезка прямой.
Перспективу отрезка общего положения можно разделить на пропорциональные части двумя способами.
Можно, пользуясь предыдущим приемом, разделить сначала перспективу горизонтальной проекции отрезка, а затем перенести полученные точки вертикальными прямыми на перспективу отрезка.
Можно применить и другой способ — построить точку схода Fl перспективы данной прямой и на горизонтали, проведенной через эту точку схода, определить точку V1, — центр соответствия (см. рис. 304).
3. Деление перспективы отрезка на основе перспективного соответствия двух прямых (рис. 290).
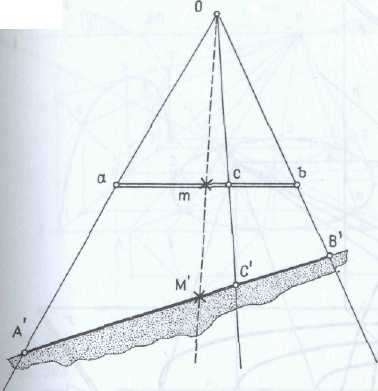
Любой отрезок и его перспективу, разделенные на пропорциональные части, можно привести в перспективное соответствие, если известны три пары соответственных точек.
Соответствие между точками двух прямых называется перспективным, если прямые, соединяющие соответственные точки этих прямых, проходят через общую точку — центр соответствия или точку зрения.
Отрезок А'В' является перспективой отрезка ab, заданного в ортогональной проекции.
Тремя парами соответственных точек являются концы отрезков и точки с и С’. Требуется привести перспективу А'В' этого отрезка в перспективное положение так, чтобы между любыми точками этих отрезков было установлено перспективное соответствие.
Выберем произвольную точку О — центр соответствия. Проведем через эту точку и точки а, b и с проецирующие прямые.
Перспективу отрезка (с помощью полоски бумаги) поместим таким образом, чтобы проецирующие лучи проходили через соответственные точки А', В' и С перспективы прямой.
Это положение и будет искомым.
Если третья, промежуточная точка не известна, необходимо определить середину M' перспективы отрезка одним из способов, указанных на рис. 288.