Параллельные прямые.

Перспекти­вы параллельных прямых пересекают­ся, т. е. имеют общую точку схода (рис. 282, а).

Для построения точки схода прямой (см. рис. 279) следует из точки зрения про­вести проецирующий луч параллельно данной прямой до пересечения с карти­ной. Следовательно, эта точка будет точкой схода для всех прямых, парал­лельных данной прямой. Точки схода горизонтальных прямых расположены на линии горизонта (рис. 282, б).

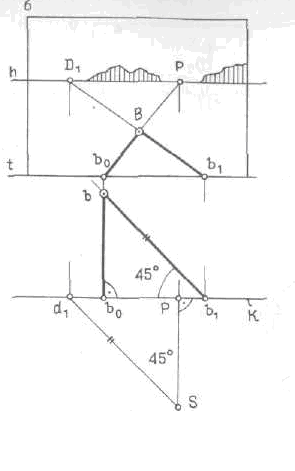
Перспектива точки.

Перспектива точки определяется как точка пересе­чения перспектив двух прямых, обычно прямых частного положения.

Из вспо­могательных прямых наиболее удобны прямые, лежащие в вертикальных про­ецирующих плоскостях, прежде всего прямые (радиальные), проходящие че­рез основание S точки зрения (см. рис. 280, б).

На рис. 283 приведены перспективы точек, построенные с помощью пересе­чения перспектив следующих пар пря­мых:

• а — перпендикулярной картине и проецирующего луча (радиальной пря­мой); высоту точки А (ее аппликату z ) откладывают в плоскости картины, где она проецируется в истинную величину, от точки а₀ — картинного следа вто­ричной проекции прямой;

• б — перпен­дикулярной картине и прямой, направ­ленной под углом 45° к картине, точка схода которой — дистанционная точка D1;

• в — проецирующего луча (радиаль­ной прямой) и горизонтальной прямой произвольного положения.

При расположении точки вблизи оси изображения перспективы вспомо­гательных прямых пересекаются под острым углом, что не обеспечивает не­обходимой графической точности.

Поэ­тому использовать в качестве точки схода главную точку картины нецеле­сообразно. В этом случае следует при­менять вспомогательные прямые, изо­браженные на рис. 283 б, в.

Перспектива плоскости.

Перспек­тива плоскости может быть построена как перспектива точек, прямых или плоской фигуры. Изображение плоской фигуры — наиболее распространенный случай. Построение перспективы, как правило, начинают с построения перс­пективы плана объекта. Рассмотрим несколько примеров построения перс­пективы плоскости.

1.Построение перспекти­вы горизонтальной плоскости

— прямоугольного четырехуголь­ника, расположенного в предметной плоскости (рис. 284).

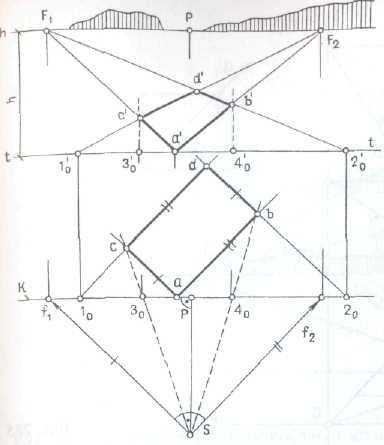
1. Для построения точек схода двух пар параллельных прямых (сторон че­тырехугольника) проведем на плане че­рез точку зрения проецирующие лучи параллельно этим прямым до пересече­ния с картиной в точках f1, и f₂ и пере­несем эти точки вертикальными пря­мыми на линию горизонта.

2. Построим на плане картинные следы 1₀ и 2₀ двух сторон четырехугольника и перенесем их на основание картины.

3. Определив на картине точки схода для каждой пары параллельных прямых и картинные следы прямых (точка а' также представ­ляет собой картинный след двух сторон четырехугольника), можно построить перспективы этих прямых.

4. Пересече­ние прямых противоположного направ­ления определит на изображении вер­шины четырехугольника и его перспек­тиву.

Если картинный след или точка схода прямой оказываются за предела­ми чертежа, следует применять в каче­стве вспомогательных перспективу ра­диальных прямых Sс и Sb, проходящих

через основание точки зрения (они вы­делены штриховыми линиями).

Перспектива горизонтальных плоскостей квадрат­ной формы, стороны которых попарно параллельны и перпендикулярны кар­тине.

Ближней стороной квадраты со­вмещены с картиной.

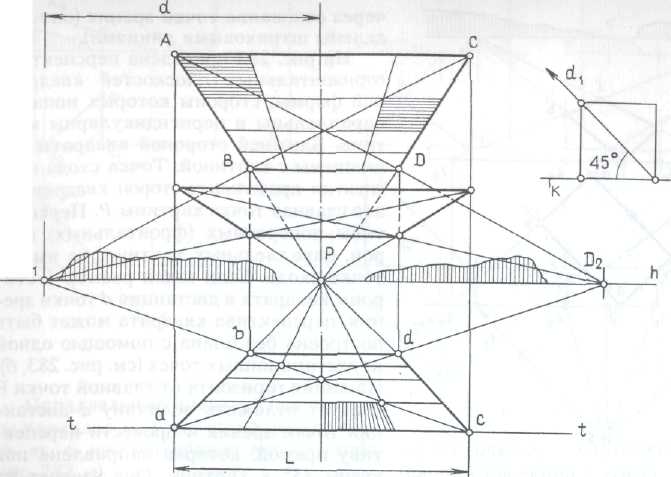
Точка схода пер­спектив продольных сторон квадрата — это главная точка картины Р. Перспек­тивы поперечных (фронтальных) сто­рон, параллельных картине, не имеют точки схода. Если задан размер L сто­роны квадрата и дистанция d точки зре­ния, перспектива квадрата может быть построена без плана с помощью одной из дистанционных точек (см. рис. 283, б).

1. На линии горизонта от главной точки Р следует отложить величину d дистан­ции точки зрения и провести перспек­тиву прямой» которая направлена под углом 45° к картине.

2. Она засечет на перспективе продольной стороны квад­рата его вершину.

3. Точки схода D1, Р, D₂ горизонтальных прямых, как и любых других горизонтальных прямых, лежат на линии горизонта.

4. Следовательно, линия горизонта по аналогии с точкой схода параллельных по аналогии с точ­кой схода параллельных прямых пред­ставляет собой линию схода горизон­тальных плоскостей.

Линией схода плоскости является перспектива бесконечно удаленной, не­собственной прямой данной плоско­сти. Она служит линией схода и всех других плоскостей, параллельных дан­ной.