Перспектива прямой линии, точки и плоскости.

Прежде чем перейти к построе­нию перспективы прямых, точек и пло­скостей, рассмотрим некоторые поло­жения геометрии, придающие необходимую общность закономерностям эле­ментарной геометрии и новым поняти­ям бесконечно удаленных точек и пря­мых, с которыми при построении перс­пективы приходится встречаться.

Дополнение евклидова пространст­ва несобственными элементами. Метод центрального проецирования рассмат­ривался в геометрическом пространст­ве, называемом евклидовым.

В евкли­довом пространстве параллельные пря­мые не пересекаются, параллельные плоскости также не пересекаются. Од­нако, как будет показано далее, приме­нение метода центральной проекции в евклидовом пространстве встречает су­щественные затруднения.

Рассмотрим центральную проекцию прямой АВ на плоскость проекций К (рис. 278). Некоторым точкам 1, 2, 3, ... прямой АВ соответствуют определен­ные точки 1’, 2', З’ ... ее центральной проекции. Такое соответствие, уста­новленное между точками прямой АВ (оригинала) и точками ее центральной проекции (изображения), называется взаимно однозначным.

Однако распространить это положе­ние на все точки соответственных пря­мых (оригинала и изображения) не уда­ется. В двух случаях произойдет нару­шение взаимной однозначности:

1) для точки-оригинала С, расположенной на проецирующем луче SC, параллельном плоскости К, не существует соответст­венной точки-изображения, так как луч SC не пересекает плоскость К;

2) для точки-изображения F’ пересечения проецирующего луча SF' с плоскостью К и параллельного прямой АВ также не существует на прямой соответственной точки-оригинала, так как луч SF па­раллелен прямой АВ.

Таким образом, точечное соответст­вие, установленное с помощью цент­рального проецирования, обладает су­щественными нарушениями, без устра­нения которых применение метода цен­тральных проекций невозможно. Это нарушение можно устранить, если до­полнить каждую прямую бесконечно удаленной или несобственной точкой. Тогда можно считать, что параллель­ные прямые пересекаются в бесконечно удаленной, несобственной точке С’. Собственными элементами принято на­зывать прямые и плоскости, располо­женные в ограниченном (конечном) пространстве. Множество прямых, при надлежащих плоскости, также будут иметь несобственные точки. Совокуп­ность несобственных точек составляет несобственную прямую плоскости. Каждая плоскость дополняется несоб­ственной прямой. По этой прямой пере­секаются взаимно параллельные пло­скости.

Рассуждая так и дальше, приходим к представлению о несобственной пло­скости пространства. Пространство, дополненное несобственными элемен­тами — точками, прямыми и плоско­стью, называется расширенным евкли­довым пространством. Поэтому вве­дение несобственных точек и прямых привело к полной разрешимости опера­ции центрального проецирования.

Эти положения находят наглядное подтверждение при построении перс­пективы параллельных прямых и пло­скостей (см. рис. 280, а и 282, б), где точка F(точка схода) перспектив парал­лельных прямых есть изображение не­собственной точки F, а линия горизон­та hh есть несобственная прямая (линия схода) предметной Т и горизонтальной Н плоскостей. Таким образом, в перс­пективе может быть получено изобра­жение бесконечно удаленных точек м прямых.

Вернемся к рис. 278. Итак, проеци­руя точки прямой АВ на плоскость К и перемещая проецирующий луч по пря­мой АВ от точки 1 в сторону точки С, можно теперь построить центральную проекцию C’ точки С, которая будет несобственной. Продолжая непрерыв­ное перемещение проецирующего луча дальше к точкам 6, 7, 8, ..., убеждаемся, что сразу после точки С проекция сле­дующей точки появится на другом кон­це центральной проекции прямой АВ. Перспектива "полупрямой" С — 8 ... создает впечатление замкнутости пря­мой. Отсюда следует, что прямая в рас­ширенном евклидовом пространстве ведет себя так, как если бы она была замкнутой подобно окружности ог­ромного радиуса.

Перспектива прямой общего поло­жения.

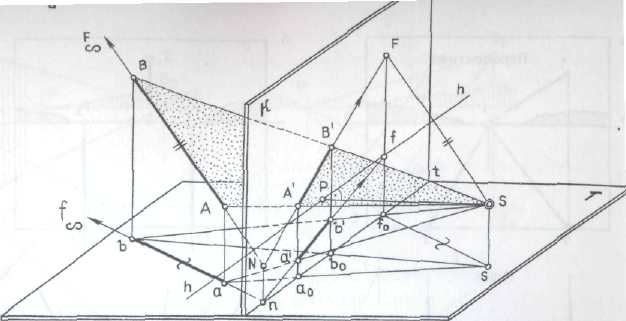
Проецирующие лучи, которые проходят через точку S и прямую АВ_Ь образуют лучевую плоскость (рис. 279, а).

Эта плоскость пересекает картину по прямой А'В', которая и является пер­спективой данной прямой.

Для постро­ения перспективы отрезка АВ прямой (рис. 279, б) достаточно определить пер­спективы точек А' и В' — концов отрез­ка, как это было сделано на рис. 276.

Соединив полученные точки прямой линией, получим перспективу А 'В' пря­мой АВ.

Однако удобнее построить перспективу прямой по двум особым ее точкам: картинному следу N прямой и точке схода F.

Картинным следом прямой назы­вается точка пересечения прямой с картиной.

Для определения картинно­го следа сначала необходимо найти след n горизонтальной проекции пря­мой, а затем на вертикали от него — след N самой прямой.

Точкой схода прямой называется перспектива бесконечно удаленной точки прямой.

Она служит точкой схо­да для всех прямых, параллельных дан­ной прямой

Для построения точки схо­да прямой надо сначала определить точку схода f ее горизонтальной проек­ции, проведя проецирующий луч парал­лельный прямой АВ до пересечения с картиной, а затем построить на плане в совмещенном положении на отрезке Sf угол  наклона прямой и полученную величину z отложить в перспективе от точки f вверх.

Положение точки схода F на картине позволяет судить о том, как расположена прямая общего поло­жения в пространстве:

• если точка нахо­дится выше линии горизонта, то прямая АВ — восходящая,

• если точка F — ниже линии горизонта (рис. 279, в) — прямая нисходящая.

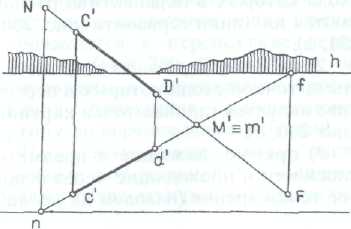
Точка М', в которой перс­пектива прямой пересекает вторичную проекцию, является перспективой гори­зонтального следа прямой.

Перспектива прямых линий частно­го положения.

Построение перспекти­вы прямых частного положения выпол­няется проще, чем построение прямых общего положения, поэтому они нахо­дят широкое применение как вспомога­тельные прямые при построении перс­пективы.

К прямым частного положения от­носительно картинной плоскости отно­сятся:

• горизонтальные прямые, точки cхода которых в перспективе располагаются на линии горизонта (рис. 280, а,281, а);

• прямые, перпендикулярные кар­тине, точкой схода которых в перспек­тиве является главная точка картины Р (рис. 280, а);

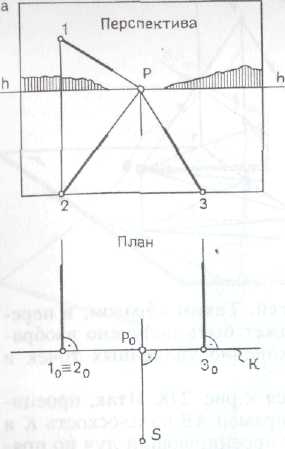
• прямые, лежащие в предметной плоскости и проходящие через основа­ние точки зрения (радиальные), а также прямые общего положе­ния, вторичные проекции которых про­ходят через основание точки зрения, изображаются в перспективе верти­кальными (рис. 280, б), поскольку они расположены в вертикальных проеци­рующих плоскостях, пересекающих картину по вертикальным прямым;

• горизонтальные прямые, распо­ложенные под углом 45° к картине, точками схода которых в перспективе являются дистанционные точки Dl и D2 (рис. 281, а);

• прямые, параллельные карте не имеют точек схода, их перспективы параллельны самим прямым (рис. 281 б). Они не имеют и картинных следов; так как не пересекаются с нею.

Плоские фигуры, параллельные картине, изображаются в перспективе подобными.