4. Перспектива поверхности враще­ния (рис. 333).

Построение в перспекти­ве очертания поверхности вращения может быть выполнено двумя способами — способом параллелей и способом меридианов.

Первый из них получил большее распространение.

На поверх­ности вращения в ортогональной про­екции проводят несколько параллелей, располагая их чаще в месте, где кри­визна очерка больше (рис. 333, а).

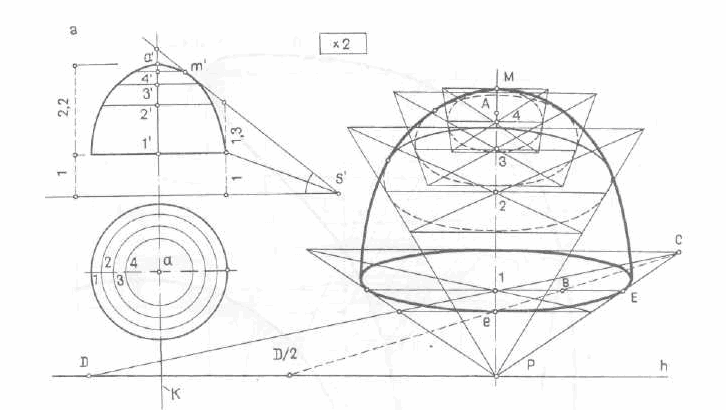
Стро­ят перспективу параллелей — четыре соосные окружности, отложив на оси центры 1, ..., 4 окружностей и вершину А поверхности (картина проведена че­рез ось поверхности).

Перспективу ок­ружностей — эллипсы — вписывают в перспективу горизонтальных квадра­тов, построенных с помощью дистанци­онной точки D или дробной точки D/2.

Прямая ВС проведена в точку D/2 че­рез середину отрезка 1E.

К перспекти­вам построенных окружностей прово­дят касательную кривую очерка повер­хности. Видимый силуэт поверхности по своим пропорциям (1 : 1,3) заметно отличается от действительных соотно­шений поверхности на фасаде (1 : 2,2).

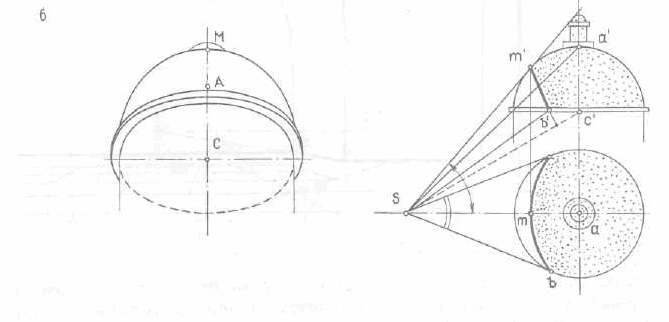
В перспективе, при восприятии с естест­венной, пониженной точки зрения, по­верхность купола как бы западает, ее вершина (точка А) оказывается скры­той, а высшей воспринимается точка М (рис. 333, б).

5. Перспектива крестового свода (рис. 334).

Крестовый свод образуется пересечением двух полуцилиндров рав­ного диаметра. Линию пересечения со­ставляют две плоские кривые — полу­эллипсы. Для построения фронтальной перспективы крестового свода (линии пересечения полуцилиндров) использу­ют две направляющие полуокружности. Одна из них расположена во фронталь­ной плоскости спереди, а другая — в профильной плоскости слева. Сначала строят вторичную проекцию линии пе­ресечения полуцилиндров — прямые АВ и CD — диагонали перспективы квадрата (штриховые линии).

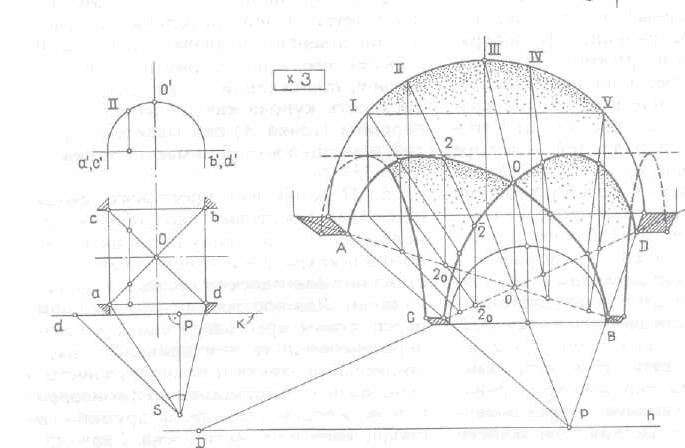
Перспек­тива линии пересечения — два полуэл­липса — может быть построена двумя способами — с помощью горизонталь­ных или вертикальных вспомогатель­ных плоскостей-посредников.

Приме­ним второй способ.

В этом случае может быть использована одна направляющая полуокружность — фронтальная.

Про­ведем пять вертикальных секущих пло­скостей, I, ..., V и рассмотрим сечение плоскостью //.

Она пересекает про­дольный полуцилиндр по образующей, перспектива которой направлена в главную точку Р, а вторичную проек­цию линии пересечения — в точках 2₀ и 2₀.

Вертикали, проведенные из этих то­чек в пересечении с образующей II, оп­ределят две искомые точки 2 и 2 линии пересечения.

Точка О — перспектива пересечения двух полуэллипсов — по­строена с помощью вспомогательной плоскости III.

Построенные точки сое­диняют плавными кривыми.

Последо­вательность соединения определяют по вторичной проекции пересечения.

Пер­спективы двух полуэллипсов и двух по­луокружностей, расположенных в профильных плоскостях, должны ка­саться одной образующей поперечного полуцилиндра (горизонтальная штри­ховая прямая).

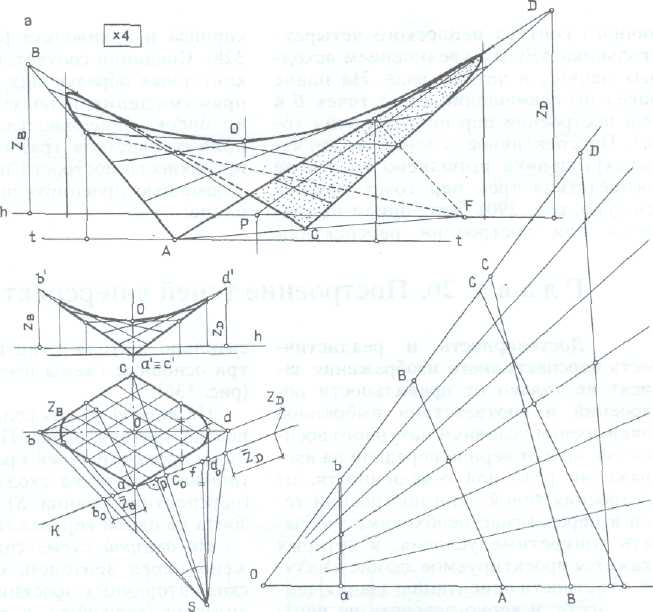
6. Перспектива поверхности гипер­болического параболоида. На рис. 335 показана перспектива отсека гипербо­лического параболоида, который пред­ставляет собой оболочку покрытия. От­сек вписан в неплоский четырехуголь­ник ABCD. Для построения перспекти­вы поверхности наиболее рациональ­ным является радиальный способ с со­вмещением высот . Сначала построена перспектива граничного контура неплоского четырех­угольника ABCD с увеличением исход­ных данных в четыре раза. На плане показаны совмещение высот точек В и D и построение перспективы этих то­чек. Перспективное деление сторон че­тырехугольника выполнено на основе соответствия трех пар точек прямых. Этот прием приме­нялся при построении перспективы карниза и архивольта. Соединив соответственные точки контурных образующих двух семейств прямыми линиями, получим перспекти­ву очерка поверхности.

Перспектива кривых участков граничного контура поверхности построена по трем точкам с помощью проецирующих прямых на плане.