Радиальный способ и способ совмещенных высот

Сущность радиального способа построения перспективы заключается в определении точек пересечения про­ецирующих лучей с картинной плоско­стью с помощью построения картинных следов прямых, перпендикулярных картине.

Этот способ поэтому называ­ется также способом следа луча.

Он на­ходит применение главным образом при построении фронтальных перспек­тив улиц, внутренних дворов, фасадов зданий с выступающими вперед частя­ми и т. д.

Рассмотрим примеры построения перспективы способом следа луча.

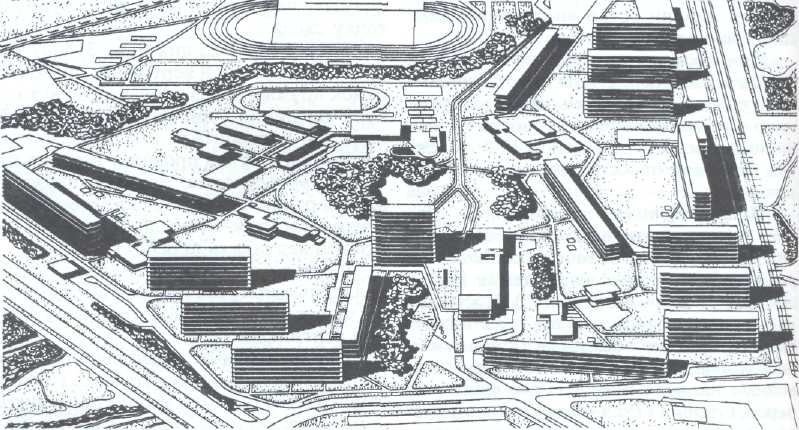
1. Построение фронталь­ной перспективы здания (рис. 306).

• Точка зрения располагается в пределах средней трети ширины фа­сада, как это было установлено ранее.

• Картина совмещена с фронтальными плоскостями выступа­ющих вперед объемов здания. Точкой схода перспективы прямых является главная точка картины Р.

• Для построе­ния перспективы точки, например точ­ки 2, сначала строят картинный след В (b) прямой 4 — b, проходящей через точку 2, отложив на перспективе высо­ту Н_II точки 2, взятую с фасада.

• Затем проводят горизонтальную S2 и фронтальную РВ проекции луча.

• Вертикаль, проведенная из точки 2₀ плана, в пере­сечении с перспективой прямой РВ (фронтальной проекцией луча) опреде­лит перспективу точки 2.

• Некоторые плоскости объекта совпадают с картин­ной плоскостью или параллельны ей; эти плоскости изображаются в перспек­тиве или в истинную величину или про­ецируются с уменьшением, оставаясь подобными своим действительным со­отношениям.

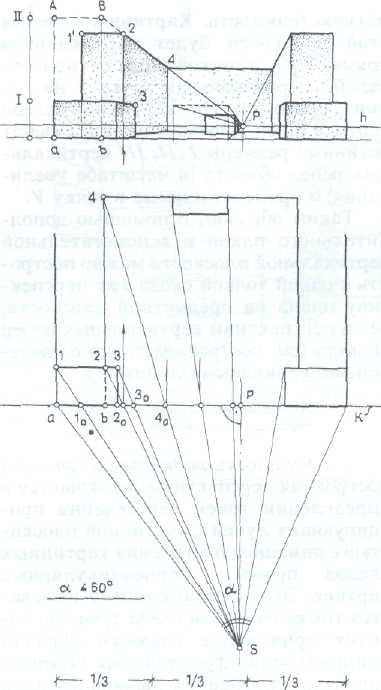
2. Построение угловой перспективы.

На рис. 307 постро­ена угловая перспектива объекта.

По­строения аналогичны предыдущему примеру, однако при построении перспективы точек, определяя картинные следы прямых, оказывается необходи­мым вычертить дополнительную фронтальную проекцию объекта в поверну­том положении.

Положительное каче­ство радиального способа состоит в компактности построений и отсутствии удаленных от поля чертежа точек схо­да.

К числу недостатков следует отне­сти малую графическую точность по­строений в средней части изображения вблизи главной точки картины Р (на­пример, построение перспективы точки 3), а также необходимость выполнений дополнительной ортогональной проекции фасада при построении угловой перспективы.

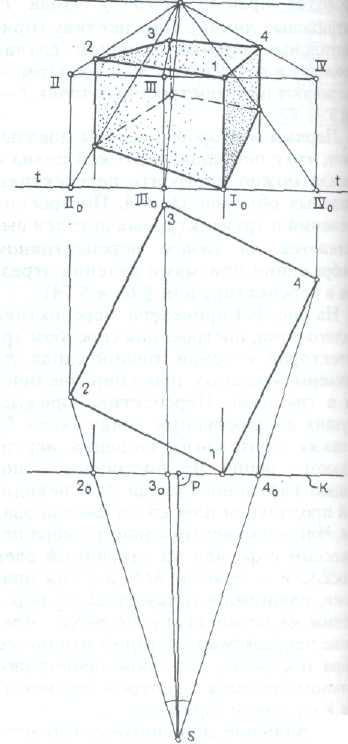
Способ совмещенных высот.

Этот способ представляет собой разновид­ность радиального способа построения перспективы с совмещением высот то­чек на плане (рис. 308) и является про­стейшим способом построения перспек­тивы. Его применение не требует зна­ния теории перспективы.

Он применя­ется при построении перспективы не­сложных объектов нерегулярной фор­мы, когда использование точек схода прямых нецелесообразно.

Несмотря на некоторую многодельность построений, этот метод выгодно отличается от ради­ального способа, основанного на приме­нении картинных следов прямых, своей простотой, а также определенной уни­версальностью.

Пользуясь совмещени­ем высот, можно построить как угло­вую, так и фронтальную перспективу без точек схода, а также перспективу объектов неправильной формы.

После определения точек пересече­ния проецирующих лучей с основанием картины для построения перспективы точки, например точки 4, расстояние от линии горизонта до фронтальной про­екции точки, взятое с фасада, совмеща­ют с планом, проводя прямую парал­лельно основанию картины. Затем из совмещенной точки 4 проводят луче­вую прямую к точке зрения. Пересече­ние этой прямой с основанием картины определяет расстояние z₄ перспективы точки 4 от линии горизонта. С целью экономии рабочего места на поле чер­тежа совмещение высот точек на плане можно производить в любую сторону (см. построение точки 2, z₂).

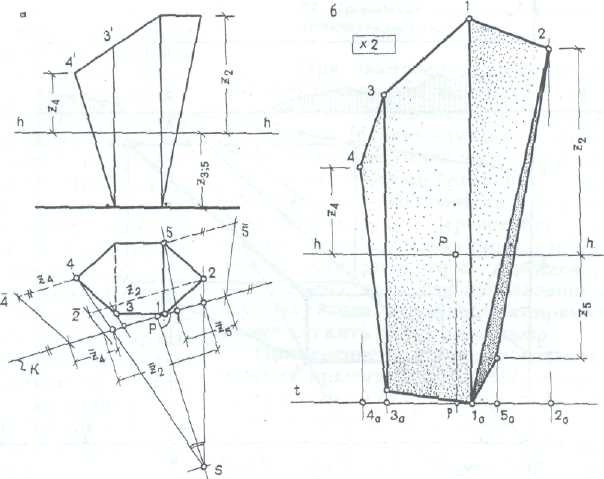
Способ прямоугольных координат и перспективной сетки.

Координатный способ построения перспективы, как и ради­альный способ, имеет ограниченное применение.

Он используется главным образом при изображении несложных объектов неправильной формы. Сущ­ность этого способа заключается в по­строении перспективы объекта, отне­сенного к прямоугольной системе коор­динат с помощью изображения в перс­пективе координатной системы (рис309).

Для построения перспективы объ­екта на план и фасад наносят оси пря­моугольной системы координат таким образом, чтобы картинная плоскость совпадала с координатной плоскостью xoz, а предметная плоскость — с коор­динатной плоскостью хоу.

При этом ос­нование картины совпадает с осью х, ось z вертикальна, ось у, перпендику­лярная картине, проходит через глав­ную точку картины.

Координатные оси, построенные в перспективе, называют перспективным масштабом.

Ось х на­зывают масштабом широт, ось z — масштабом высот, ось у — масштабом глубины.

По осям x и z откладывают натуральные единицы измерения.

По оси у их откладывают с помощью дис­танционной точки D.

Так, для построе­ния перспективы точки А — одного из концов отрезка АВ — на осях х и z от­кладывают абсциссу и апликату точки А.

Ординаты точки в перспективе стро­ят с помощью дистанционной точки, от­кладывая истинную величину ордина­ты у_a на основании картины, и проводят прямую в точку D.

Она засечет на оси у ординату точки а_у.

Затем проводят вспомогательные горизонтальные и вертикальные прямые и получают вто­ричную проекцию а точки и ее перспек­тиву А.

Способ перспективной сетки.

Этот способ является разновидностью коор­динатного способа.

Он также основан на применении перспективных масшта­бов. Способ сетки применяют при по­строении "планировочных" перспектив с высоким горизонтом при проектиро­вании градостроительных и промыш­ленных объектов, расположенных на значительной территории.

После выбора точки зрения (рис. 310, а) на исходный план объекта нано­сят сетку фронтально расположенных квадратов со стороной, равной 1, 2, 5,10, ...м.

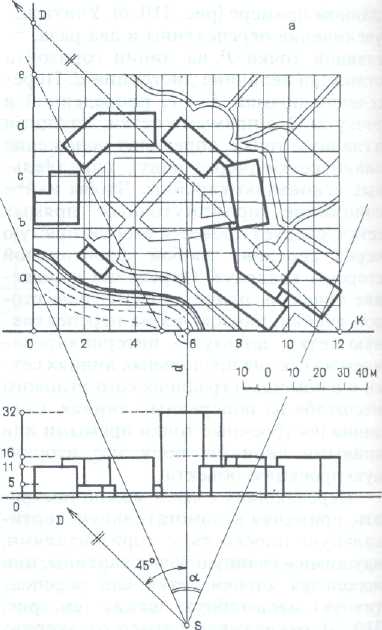
По сторонам сетки ставят буквен­ные и цифровые обозначения ячеек.

На фасаде отмечают размеры высот объек­тов.

Перспективную сетку строят с по­мощью дистанционной точки или дроб­ной дистанционной точки D/2, как в данном примере (рис. 310, б).

Учитывая увеличение перспективы в два раза, от главной точки Р на линии горизонта отложена величина дистанции d.

Пере­сечение прямой 5 — е_, проведенной в точку D/2, с прямыми сетки, идущими в главную точку, определит положение линий сетки (через одну), параллель­ных основанию картины. Чтобы найти положение промежуточных прямых сетки, следует провести вторую прямую через середину любой фронтальной стороны квадрата.

Определив положе­ние точек на плане относительно сто­рон ячейки, наносят их на перспектив­ную сетку, пользуясь интерполирова­нием на глаз на продольных линиях сет­ки и с помощью графического углового масштаба на поперечных линиях.

Сое­динив построенные точки прямыми или кривыми линиями, получают вторич­ную проекцию объекта.

Перспективу высот можно постро­ить, применяя вспомогательную верти­кальную плоскость с горизонталями, идущими в главную точку картины, или используя ячейки сетки как перспек­тивную масштабную шкалу , откладывая размер от вторич­ной проекции точки параллельно попе­речным линиям сетки аналогично спо­собу совмещенных высот.

При построении вторичной проек­ции точек и перспективы высот необхо­димо учитывать отметки соответствую­щего участка рельефа местности — ве­личину превышения оснований точек над условной плоскостью, принятой за нулевую.