
- •5. Равенство двойного и повторного интеграла.
- •6. Замена переменных в двойном интеграле. Линейная замена.
- •7. Переход к полярным координатам в двойном интеграле.
- •8. Геометрические приложения 2-го интеграла: площадь плоской фигуры, объем цилиндроида, площадь поверхности.
- •9. Определение числового ряда, его сходимости и расходимости. Необходимое условие сходимости.
- •10. Признак сравнения (элементарная и предельная форма).
- •15. Степенной ряд. Т. Абеля. Радиус и интервал сходимости. Стр-ра области сходимости.
- •16. Определение и сходимость ряда Маклорена.
- •17. Ряды Маклорена функций ех, sin X, cos X.
- •27.Дискретная св, ряд распределения, свойства функции распределения
- •28.Непрерывная св, плотность вероятности. Свойства функции распределения и плотности
- •29.Функция случайной величины вида , формулы для и
- •30.Функция случайной величины вида , формулы для и
- •31.Математическое ожидание и дисперсия дискретной св: определение, вычисление и свойства
- •32.Математическое ожидание и дисперсия непрерывной св: определение, вычисление и свойства
- •33.Биномиальный закон распределения: определение, числовые характеристики
- •34.Пуассоновский закон распределения: определение, числовые характеристики
- •35.Связь биномиального и пуассоновского законов распределения
- •36.Равномерный закон распределения: определение, числовые характеристики
- •37.Определение функции Лапласа и ее свойства
- •38.Нормальный закон распределения: определение, числовые характеристики. Вероятность попадания в интервал
- •39.Двумерная случайная величина, закон распределения, функция распределения и ее свойства
- •40.Дискретная двумерная св. Форма записи закона распределения, законы распределения компонент
36.Равномерный закон распределения: определение, числовые характеристики
Говорят, что непрерывная случайная
величина X имеет равномерное
распределение на отрезке ab,
если ее плотность вероятности f(x)=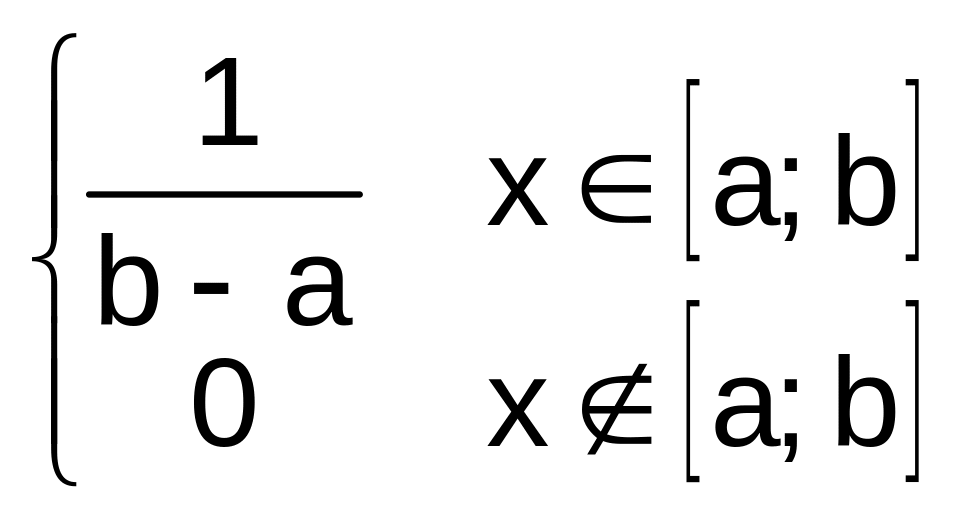 (1).
(1).
M(X)=![]() =
=![]() f(x)dx=
f(x)dx=![]()
![]() dx=
dx=
![]() =
=![]()
![]() =
=![]()
= (2)
![]()
![]()
f(x)=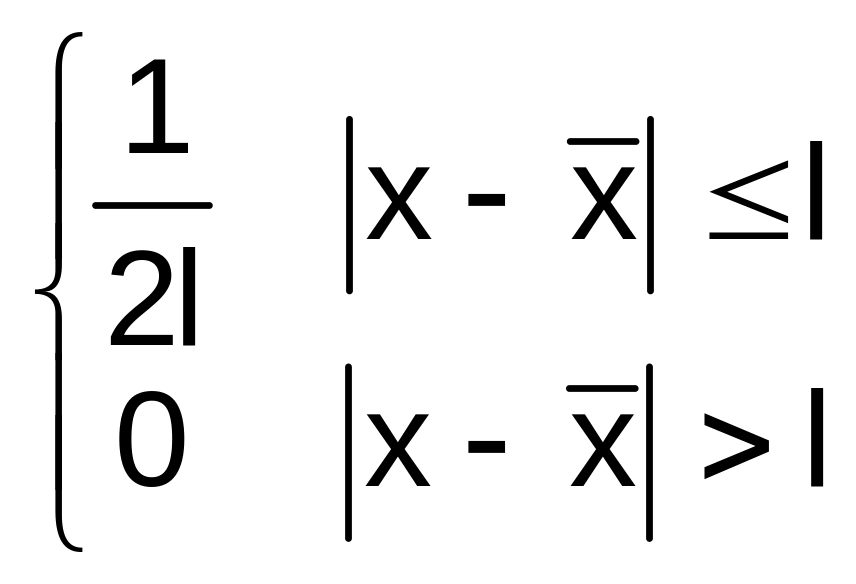 (3). (3) – каноническая формула равномерного
распределения.
(3). (3) – каноническая формула равномерного
распределения.
D(X)=σ2=m2-m12=![]() f(x)dx-(
)2=
f(x)dx-(
)2=![]()
![]() dx-(
)2=
dx-(
)2=![]()
σ2=![]() ;
σ=
;
σ=![]()
F(x)=![]() (x)dx=
(x)dx=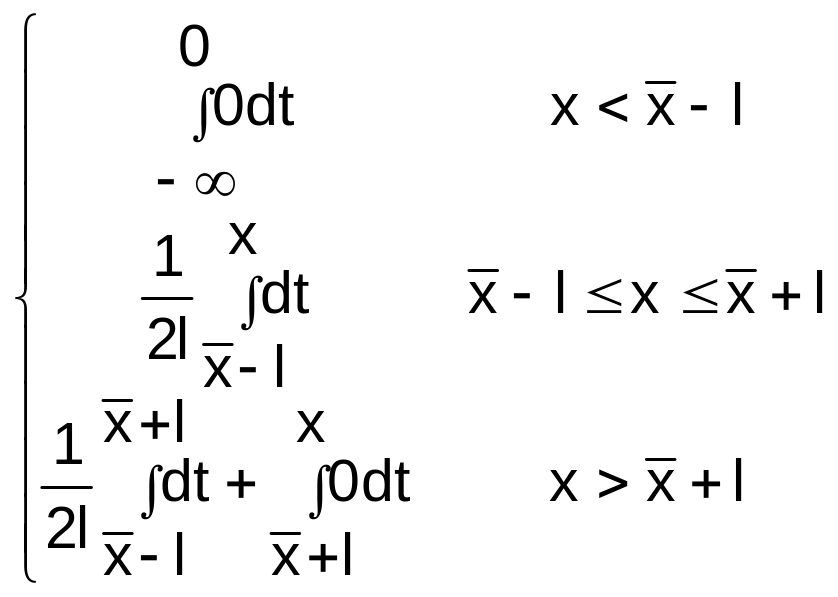 =
=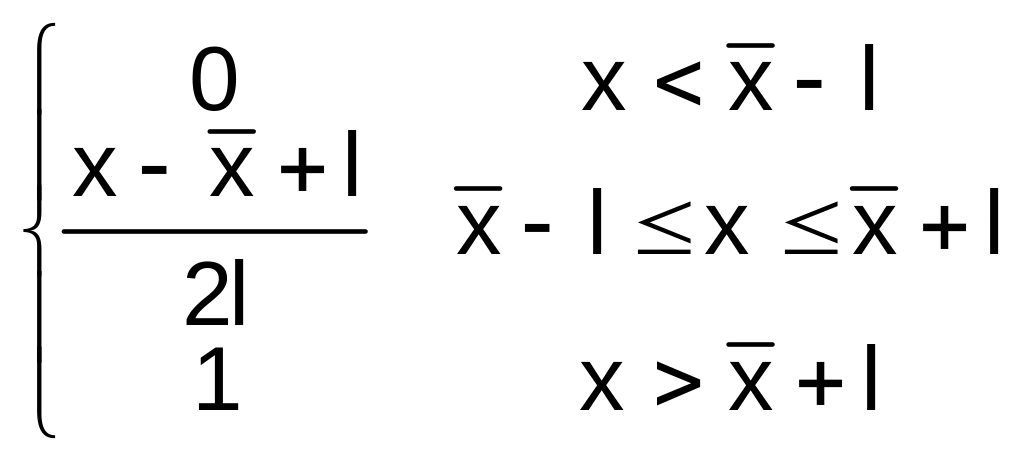
Ex(u)=M(eiux)=![]() f(x)dx
f(x)dx
Y=![]() =X-
;
M(Y)=0
=X-
;
M(Y)=0
fy(y)=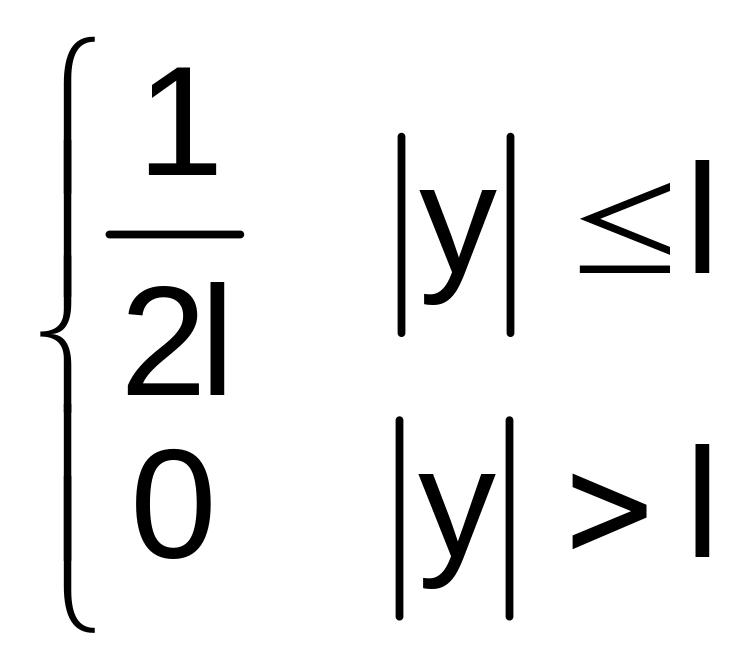
X=Y+
Ex(u)=![]() Ey(u)
Ey(u)
Ey(u)=
![]() dy=
dy=
![]()
![]() =
=![]()
![]() =
=![]() ;
Ex(u)=
;
Ex(u)=
37.Определение функции Лапласа и ее свойства
Функция Лапласа:
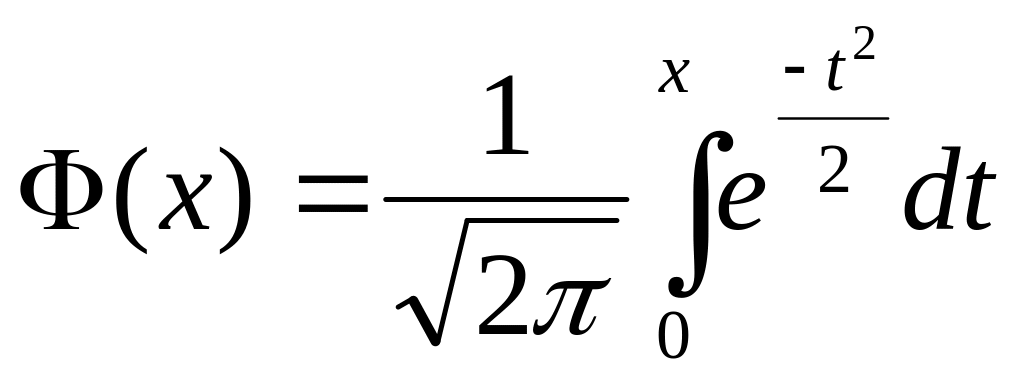
Свойства:
1.Ф(-х)=-Ф(х)
2.Ф(+∞)=1/2 (при больших х: Ф(х)≈1/2
38.Нормальный закон распределения: определение, числовые характеристики. Вероятность попадания в интервал
ξ=αξ0+β (α>0)
β→а, α→σ (σ>0)
![]()
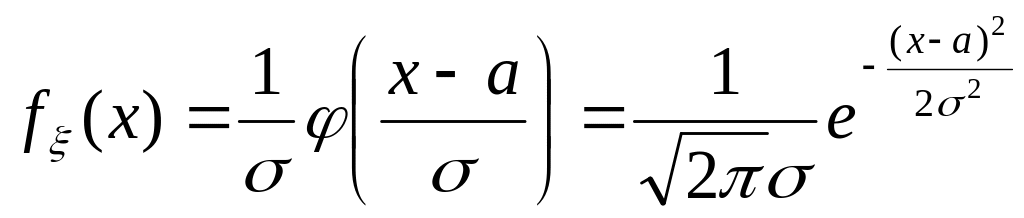
Закон распределения, определяемый плотностью вероятности fξ - нормальный закон распределения с параметрами a,σ.
M(ξ)=a
D(ξ)=σ2
![]()
39.Двумерная случайная величина, закон распределения, функция распределения и ее свойства
Ξ=(x1;x2) - двумерная СВ.
Компоненты двумерной СВ - ξ, η (ξ=х, η=y).
Пусть Ξ=(ξ;η) - двумерная СВ, ее функция распределения - функция двух переменных:
![]()
(ξ<x, η<y) можно рассматривать как попадание в бесконечный прямоугольник Д.
Свойства функции распределения повторяют свойства одномерной функции распределения:
1).F(-∞;y)=F(x;-∞)=0.
2).F(+∞;+∞)=1.
3).F(x) возрастает по каждой переменной
4).F(x) непрерывна слева по каждой переменной
p(a≤ξ<b, c≤η<d)=FΞ(b;d)+FΞ(a;c)-FΞ(a;d)-FΞ(b;c)
![]()
40.Дискретная двумерная св. Форма записи закона распределения, законы распределения компонент
Для описания закона распределения можно использовать ряд распределения:
![]()
pi=p(ξ=xi;η=yi)
удобнее отдельно рассматривать значение компонентов: ξ:x1,...,xm; η=y1,...,yn
pij=p(ξ=xi; η=yj)
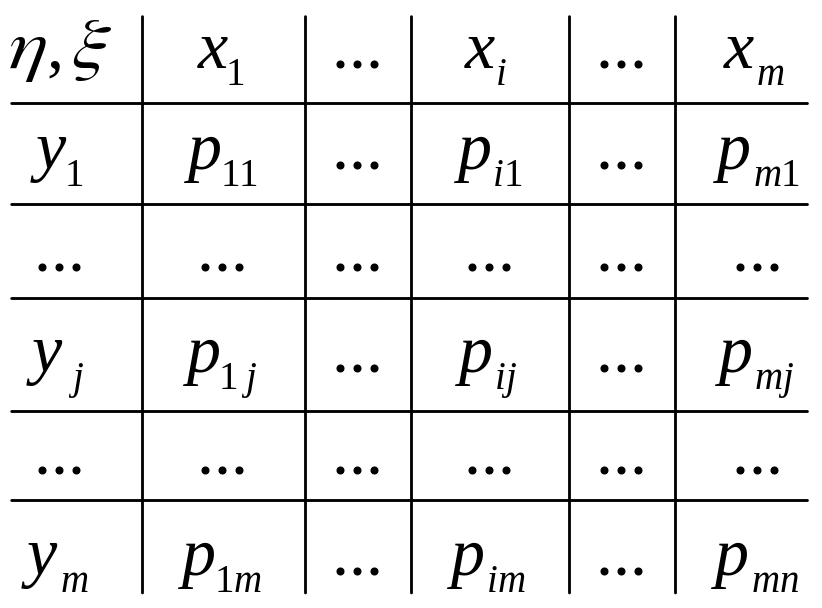
![]() ,
,
![]()
![]() ,
,
![]()
