
- •Базовые понятия математической логики
- •Алгебра высказываний
- •Формулы алгебры высказываний
- •Совершенные нормальные формы
- •Булевы функции Основные свойства и теоремы
- •Математическая модель представления релейно-контактных схем с помощью булевых функций
- •Сумматоры.
- •Четвертьсумматор
- •Двоичный полусумматор
- •Одноразрядный двоичный сумматор.
- •Заключение
Формулы алгебры высказываний
Переменные, вместо которых можно подставить высказывание, то есть переменные, пробегающие множество высказываний, называют пропозициональными переменными.
Определение формулы алгебры высказываний:
Каждая отдельно взятая пропозициональная переменная, есть формула алгебры высказываний.
Если
 некоторые формулы алгебры высказываний,
то
некоторые формулы алгебры высказываний,
то
 ,
являются формулами алгебры высказываний.
,
являются формулами алгебры высказываний.Никаких других форм алгебры высказываний, кроме полученных в пунктах 1 и 2, нет.
Все формулы можно разделить на следующие 4 категории:
1.Формула алгебры высказываний называются выполнимой, если существует такая интерпретация, при подстановке которой формула обращается в истинное высказывание.
2.Формула алгебры высказываний называется опровержимой, если существует такая интерпретация, при подстановке которой формула обращается в ложное высказывание.
3. Формула алгебры высказываний называется тавтологией или тождественно-истинной, если на любой интерпретации она обращается в истинное высказывание.
4. Формула алгебры высказываний называется противоречием или тождественно-ложной, если при подстановке любой интерпретации она обращается в ложное значение.
Совершенные нормальные формы
Совершенная нормальная форма данной формулы – это формула, равносильная данной, содержащая только отрицания, конъюнкции и дизъюнкции.
Конъюнктивный
одночлен
или конъюнт
от переменных
 ,
, ,…,
,…,
 –
это конъюнкция этих переменных или их
отрицаний.
–
это конъюнкция этих переменных или их
отрицаний.
Конъюнктивный
(дизъюнктивный)
одночлен
от переменных
,…,
называется совершенным,
если от каждой пары
 –
¬
входит ровно 1 представитель. Например,
(¬
)
۸
۸
–
¬
входит ровно 1 представитель. Например,
(¬
)
۸
۸ ).
).
Дизъюнктивной
нормальной формой (ДНФ)
называется дизъюнкция конъюнктивных
одночленов, т.е. выражение вида
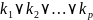 ,
где
,
где
 i=1…p,
-
конъюнктивный одночлен.
i=1…p,
-
конъюнктивный одночлен.
Конъюнктивной
нормальной формой (КНФ) называется
конъюнкция дизъюнктивных одночленов,
то есть выражение вида
 i=1…e
i=1…e
Нормальная форма
от переменных
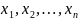 называется совершенной(СДНФ,СКНФ),
если в нее входят только совершенные
одночлены от этих переменных.
называется совершенной(СДНФ,СКНФ),
если в нее входят только совершенные
одночлены от этих переменных.
Алгоритм приведения формулы к СДНФ (СКНФ):
Выбрать все наборы переменных, при которых формула истинна (ложна).
Для каждого набора выписать совершенный конъюнктивный (дизъюнктивный) одночлен, логическое значение которого равно 1 (0) на нем и только на нем.
Полученные одночлены соединить знаками дизъюнкции (конъюнкции)
Булевы функции Основные свойства и теоремы
Булева функция – функция, аргументы которой заданы на двухэлементном множестве {0, 1}, и сама она принимает значения на том же множестве.
Аргументы булевых функций принято обозначать строчными латинскими буквами: f(x1, x2, …, xn) : {0, 1}n → {0, 1}.
Теорема: Всякая булева функция может быть представлена в виде суперпозиции конъюнкции, дизъюнкции и отрицания (причем знак отрицания стоит только непосредственно около переменной и не стоит после внутренних скобок).
Значит, каждой формуле алгебры высказываний можно поставить в соответствие булеву функцию. Здесь же стоит отметить, что также термины СДНФ и СКНФ можно применить и к булевым функциям.
Свойства булевых функций, необходимые при их преобразовании:
Название свойства |
В применении к дизъюнкции |
В применении к конъюнкции |
Идемпотентность |
xVx = x |
xx = x |
Коммутативность |
xVy = yVx |
xy = yx |
Ассоциативность |
(xVy) Vz = xV(yVz) |
(xy)z = x(yz) |
Дистрибутивность |
xV(yz) = (xVy)(xVz) |
x(yVz) = (xy)V(xz) |
Свойство единицы |
xV1 = 1 |
x*1 = x |
Свойство нуля |
xV0 = x |
x*0 = 0 |
Поглощение |
xV(yx) = x |
x(yVx) = x |
|
xVx’ = 1 |
xx’ = 0 |
Законы де Моргана |
(xVy)’ = x’y’ |
(xy)’ = x’Vy’ |
Отрицание отрицания |
x’’ = x |
|
Взаимосвязь функций |
xVy = (x→ y)→ y |
|
|
xVy = x’→ y |
|
|
x→ y = x’Vy |
|
|
x ↔ y = (x→ y)(y→ x) |
|
Принцип работы релейно-контактной схемы
Реле́ — электромагнитный аппарат (переключатель), предназначенный для коммутации электрических цепей (скачкообразного изменения выходных величин) при заданных изменениях электрических или не электрических входных величин. Широко используется в различных автоматических устройствах.
Различают электрические, пневмати-ческие (температурные), механические виды реле, но наибольшее распространение получили электрические (электромагнит-ные) реле.
Якорь — пластина из магнитного материала, через толкатель управляющая контактами. При пропускании электрического тока через обмотку электромагнита возникающее магнитное поле притягивает к сердечнику якорь, который через толкатель смещает и тем самым переключает контакты. Переключатели могут быть замыкающими, размыкающими, переключающими.

Под релейно-контактной
схемой
понимают устройство из проводников и
двухпозиционных контактов, через которое
полюсы источника тока связаны с некоторым
потребителем. Контакты могут быть
замыкающими или размыкающими. Каждый
контакт подключен к некоторому реле
(переключателю). Когда реле срабатывает
(находится под током), все подключенные
к нему замыкающие контакты замкнуты, а
размыкающие, с оответственно,
разомкнуты; в противном случае –
наоборот.
оответственно,
разомкнуты; в противном случае –
наоборот.
