11) Физическое моделирование

Представляет собой набор электрических элементов (R, L, C, E), который позволяет создать принципиальную схему, работа которой соответствует некоторым реальным процессам.

Определяется результ. f

С помощью заданной физической модели мы получим аналогичную картину затухающих колебаний.

Для того, чтобы обе картины колебаний процесса были похожи, необходимо подобрать параметры физической модели – R, L, C.

Для создания физических моделей используются аналоговые вычислительные машины. Итогом её работы является создание значений E, L, R, C. Далее электрические параметры или значения элементов пересчитываем в механические.

Физические модели имеют следующие достоинства:

1. простота

2. наглядность

Недостатки:

1. сложность подбора параметров

2. не все модели опубликованы

12) Натурное моделирование в рэс.

Натурная модель представляет собой модель в натуральную величину изделия.Затем ее испытывают при различныз воздействиях.На эксп-т в РЭ осущ-ся путем испытания реальных конструкций.Изделие берется с конвейера и проходит испытание.

Достоинства:

1. практически соответствуют реальным объектам

Недостатки:

1. дороговизна

2. требует большого обслуживающего персонала

13) Математическое моделирование

Математические модели основаны на использовании аналитических выражений функционир РЭС. Разрабатываются с использованием реальных процессов путем их аппроксимации.

y=kx

1. таблично

2. графики

3. уравнение

Задачу построения мат модели сводим к построению выражения ур-я (аппроксимация)

1. Макс. Погрешность построения модели

А) на глаз

Б)на опр-ть погреш-ть в каждую т

В) чаще по макс. Знач

+ Просто наглядность

- низкая точность

14) Виды аппроксимаций

1. Аппроксимация процессов в РЭС уравнением прямых

2. Аппроксимация процессов в РЭС простейшими тригонометрическими функциями

3. Аппроксимация процессов в РЭС степенным полиномом

4. Аппроксимация процессов в РЭС рядом Фурье (по гармоникам)

5. Аппроксимация процессов в РЭС рядом Фурье (по составляющим гармоник)

15) Аппроксимация процессов в рэс уравнением прямых

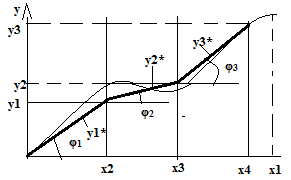
1)y=k₁x при 0 ≤ x ≤ x₂

k₁=tgφ₁

2)y=k₂x при x₂ ≤ x ≤ x₃

k₂=tgφ₂

3 y=k₃x при x₃ ≤ x ≤ x₄

k₃=tgφ₃

Чтобы модель была верной она должна соотв-ть погрешностям

Для проверки модели на адекватность необх проверить мат модель в каждой точке исх прямой,затем в завис-ти от принятого решения проводить расчет каждой точки прямой.

-условие аппроксимации Возможны 3 случая:

1)если ≤ ,то математическая модель верна(адекватна исходному процессу)

2)если ,то математическая модель не верна

3)

16) Аппроксимация процессов в рэс простейшими тригонометрическими функциями

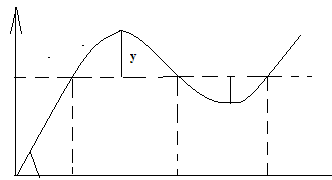
1)y^*=kx при 0 ≤ t ≤ t₁

k=tgφ

2) y^*=y₀+Δysin((2π/t₃-t₁)*t) при t₁ ≤ t ≤ t₂

T=t₂-t₁ ω=2π/T

Для проверки полученной модели на адекватность необходимо на данном графике восстановить математическую модель по точкам.

В точках где расхождение наибольшее необходимо посчитать погрешность

=(y-y^*)/ y^* ≤ , y- текущее значение

1) если ≤ ,то математическая модель верна(адекватна исходному процессу)

2) если ,то математическая модель не верна

3)

Достоинства:наглядность,простота.Недост:низкая точность на уч-ках отр коэф-тов возможны субъект ошибки