24) Характеристики отказов в рэс
При большом количестве элементов в изделии, либо изделий отказы преимущественно происходят случайно, и для расчетов надежности необходимо знать с какой частотой появляются отказы, какого типа, а лучше представлять по какому закону эти отказы изменяются.
Характеристики отказов:
- Математическое ожидание М[X]
- Дисперсия D[X]
- Среднеквадратическое отклонение δ[X]
- Коэффициент вариации ς [X]
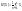
Математическое ожидание – это среднее значение случайной величины в генеральной совокупности; оно характеризует центр распределения Х.
Дисперсия – это среднее значение квадрата отклонения случайной величины от ее математического ожидания. Она характеризует рассеивание Х. Чем больше рассеиваются отдельные значения случайной величины, тем больше будет дисперсия.
Среднеквадратическое отклонение – так же, как и дисперсия характеризует рассеивание случайной величины Х.
Коэффициент вариации – отношение, которое исчисляется в процентах и характеризует рассеивание случайной величины Х в относительных единицах.
Допуски: б, 2б, 3б.
Задача технолога: установка разброса параметра (±10%) со значением среднеквадратического отклонения. Разброс и среднеквадратическое отклонение могут отличаться в 2-3 раза. Исходя из этого технолог, при изучении РЭС, приходит к задаче знать закон отказов РЭС (W[X]).
25.Законы распределения отказов рэа.
Очевидно, что при большом количестве изделий отказы происходят случайно и для расчета надежности необходимо знать, с какой частотой появляются отказы, какого типа, а лучше представлять по какому закону эти отказы изменяются.
Характеристики отказов:
1)Математическое ожидание M[x]
2)Дисперсия D[x]
3)Среднее квадратическое отклонение [x]
4)Коэффициент вариации [x]
Для примера рассмотрим математическое ожидание для резистора С2-23-0,125-10к+/-10%
1 – теоретическая кривая
2,3 – практические кривые
Закон распределения характеризует качество нашей работы. Если МО совпадает с номиналом резисторов, то это значит, что процесс идет нормально. Если же Мо отличается от номинала, то это говорит, что это смещённая оценка и её необходимо уменьшать. Смещённая оценка приводит к появлению брака в зависимости от её величины. Задача технолога всё время контролировать этот процесс, уменьшая величину смещения.
Доверительный интервал
Дисперсия на графике не изображается из-за другой размерности.
В задачи технолога входит установка разбросов параметров (+/- 10%) со значением среднего квадратичного отклонения. Разброс и среднее квадратичное отклонение могут отличаться в 2-3 раза (R=3).
Исходя из изложенного, важнейшей задачей при разработке РЭС является получение законов отказа РЭС W(x). Они должны быть построены на основании следующих сведений:
1.Наличие отказов РЭА при изготовлении.
2.Появление отказов в процессе настройки, изготовления и испытания РЭУ.
3.Наличие отказов в процессе эксплуатации РЭС.
Полученная выборка должна отражать характер распределения показателей номинала резистора. Выборка производится по специальным методикам, которые гарантируют достоверность расчетов.
Получение M[x], [x] из всего массива приводит к большим временным затратам, поэтому существуют методы уменьшения объема экспериментальных данных:
1.Уменьшение повторных вариант.
2.Выскакивающие кратные варианты.
3.Методика оценки погрешностью.
В этой методике происходит округление с точностью до, например, 1%. Затем проверяются снова 1 и 2 пункты. Объем массива уменьшается на 70-80%. Массив же из оставшихся 20% уже можно рассматривать.
Более подходящий вариант – строить законы распределения отказов. Для получения W(x) в виде уравнения необходимо эти данные аппроксимировать. Существует 24 закона распределения РЭС. В основном используются 6 законов – биноминальный, Пуассона, экспоненциальный, Вейбулла, нормальный и нормально-логарифмический законы.
Исходя из законов распределения W(x) необходимо определить характеристики случайного процесса – МО, дисперсию и среднего квадратичного отклонения. Эти характеристики можно определить по данным статистики, но это бы заняло много времени.