§10. Квазизамкнутость и статистическая независимость подсистем

Р ассмотрим систему состоящую из некоторого числа подсистем.

Даны две подсистемы и их область контакта. Взаимодействие между подсистемами идёт через границу, через приграничный слой в который проникает взаимодействие.

Чем больше время наблюдения, тем глубже проникает взаимодействие в подсистемы. Чем меньше время, тем уже этот слой.

Если слой очень узок, то взаимодействием можно пренебречь, в течение достаточно малого промежутка времени. Такие системы называются квазизамкнутыми.

С точки зрения теории вероятностей вводят понятие статистической независимости.

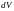- обладает свойством мультипликативности, т.е. её можно разбить на произведение элементарных объёмов подсистем:

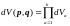
Здесь - это подсистемы.

В общем случае 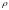- немультипликативна. Но для статистически независимых подсистем тоже мультипликативна:

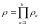
На языке средних:

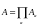
Здесь 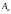- это функция координат -той подсистемы, тогда:

Тогда можно усреднять параметры, относящиеся к переменным данной подсистемы.

Вероятность 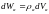, тогда тоже разбивается на .

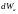Статистическую независимость обычно рассматривают при .

§11. Принцип равновероятности микросостояний

Бывает необходимо подсчитать число микросостояний, которые отвечают данному макросостоянию. Принцип равновероятности говорит, что все микросостояния, реализующие данное макросостояние, равновероятны (иногда в этом определении добавляют – для замкнутой системы).

§12. Статистический вес макросостояния

Статистический вес макросостояния – это число микросостояний, реализующих данное макросостояние.

§13. Статистическая энтропия

Вводится понятие энтропии:

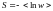- на языке плотности вероятности.

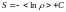- на языке функции распределения.

Оказывается, что

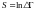
где - статистический вес макросостояния.

§14. Теорема Лиувилля

Утверждается, что функция есть интеграл движения:

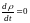
С помощью этой теоремы далее делаются выводы, которые приводят к получению функции или .

Если рассматривается случай квантовой статистики, то:

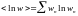, где ( - это номер состояния)

А среднее:

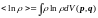, где

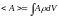
Из теоремы Лиувилля извлечём свойство:

Так как - интеграл движения, то она может быть представлена через комбинацию имеющихся у системы интегралов движения , т.е. число интегралов движения – конечное число.

Для простоты часто рассматривают так называемое микроканоническое распределение.

В случае квазизамкнутых статистически независимых систем для плотности вероятностей мы писали:

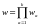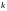, - число подсистем

И для :

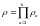-это следствие статистической независимости подсистем.

Для квантового случая пишут , -индекс подсистемы, - номер квантового состояния.

Тогда 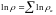, т.е. логарифм от есть величина аддитивная.

Из теоремы Лиувилля имеем:

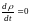, - интеграл движения

т.е. можно получить как суперпозицию интегралов движения. Для квазизамкнутых систем (в частном случае) имеем: - интеграл движения, 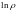- аддитивная величина.

Тогда можно представить как суперпозицию аддитивных интегралов движения.

В большинстве случаев ограничиваются одним из семи интегралов движения, а именно энергией. Для -ой системы можем записать:

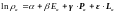
В этом выражении 7 интегралов движения: один в энергии, три в импульсе и три в моменте импульса.

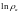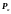Когда систему помещают в жёсткий ящик, где она не может ни вращаться, ни перемещать, то зависимость от и пропадает, и остаётся:

здесь и - произвольные константы.

В силу макроскопичности системы, влияния граничных условий ящика на общее термодинамическое состояние нет, есть лишь влияние в тонком приграничном слое.

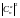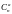В квантовом случае, можно взять равной , где - это коэффициенты разложения волновой функции по собственным функциям оператора Гамильтониана (оператора энергии).