§5. Два способа усреднения в статистической физике

Будем иметь дело со стационарными процессами.

Рассмотрим случайную величину 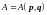, где и это динамические переменные (их штук). Но можно рассматривать и случайную величину , где - время (это одна переменная).

Усреднение по времени производим так:

(**)

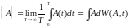Если - случайная величина, то её усреднение соответствует усреднению по фазовой траектории в фазовом пространстве.

Зависимость координат от времени в фазовом пространстве определяется фазовой траекторией.

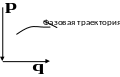
Усреднение по времени имеет основой эксперимент, т.к. экспериментатор наблюдает случайную величину во времени.

Назовём временем релаксации. Если T» , то предел (**) хорошо согласуется с практикой. И тогда принимают .

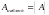Усреднение по времени, однако не удобно в теории, это усреднение по одной реализации.

Другое усреднение – статистическое. Оно основано на усреднении случайной величины как функции и .

Каждой точке фазового пространства ставится в соответствие величина ( как функция и ). Потом вводится вероятность попадания этой точки в элементарный объём фазового пространства:

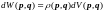
здесь 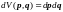- элементарный объём фазового пространства.

Говорят, что 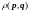- это функция распределения, определяющая плотность вероятности попадания точки в элементарный объём.

И вводится понятие статистического среднего, или среднего по ансамблю:

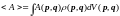
§6. Понятие ансамбля систем

Имеем совокупность макроскопических идентичных систем, именуемых ансамблями. Можем говорить, что конкретная точка фазового пространства соответствует конкретному состоянию одной из систем этого ансамбля.

У систем может быть различное динамическое состояние, так как точки перемещаются в пространстве. Хотя число точек, поля и т.п. у систем будут одинаковыми. Это и будет ансамблем, если таких систем будет неограниченно много.

Часто, т.к. рассматриваются стационарные процессы, то фазовая траектория очень длинная (бесконечная), тогда говорят, что фазовую траекторию, при рассмотрении предела , можно разбить на достаточно длинные траектории, которым можно приписать системы из ансамбля.

§7. Эргодическая гипотеза

Согласно эргодической гипотезе, для наблюдаемых величин в статистической физике водится:

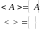
Процессы или поля для которых удовлетворяется это равенство называют эргодическими.

- это усреднение по пространству реализаций, где 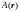-случайное поле, т.к. здесь больше одной переменной у

- усреднение по аргументам, которые «сидят» в . - это случайный процесс, т.к. одна переменная в .

§8. Равновесное состояние системы

Для стационарных процессов в случае систем с большим числом степеней свободы обнаруживается (где процесс ), что в процессе измерения величины , она основное время пребывает в состоянии, имеющим значение близкое к числу 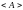(которое практически не отлично от ).

Система длительное время пребывает в состоянии со значением . Это значение представляется, таким образом, наиболее вероятным значением случайной величины .

Состояние системы, описываемое наиболее вероятными значениями макропараметра, называется равновесным. Стационарная макросистема основное время пребывает в равновесном состоянии, хотя бывают кратковременные флуктуации.

В термодинамике, во всех термодинамических соотношениях, используются равновесные состояния. Например, под понимают (пишут , а подразумевают ).