
- •§1. Экспериментальные основы квантовой механики
- •§2. Классическое и квантовое описание системы
- •[§3.] Принцип неопределенности
- •[§4.] Полный набор динамических переменных
- •[§5.] Постулаты квантовой механики
- •§6. Роль классической механики в квантовой механике
- •[§7.] Волновая функция и ее свойства
- •[§8.] Принцип суперпозиции состояний
- •§12. Среднее значение измеряемой величины
- •§13. Вероятность результатов измерения
- •[§15.] Операторы координаты , импульса , момента импульса , энергии .
- •[§ 19.] Волновое уравнение
- •[§ 24.] Оператор Гамильтона различных систем
- •§ 25. Стационарное состояние различных систем
- •[§ 28.] Собственный механический момент (спин)
- •§1. Статистическое описание систем с большим числом степеней свободы
- •§3. Микро- и макро- параметры системы.
- •§4. Свойство эргодичности системы.
- •§5. Два способа усреднения в статистической физике
- •§6. Понятие ансамбля систем
- •§7. Эргодическая гипотеза
- •§8. Равновесное состояние системы
- •§10. Квазизамкнутость и статистическая независимость подсистем
- •§15. Микроканоническое распределение Гиббса
- •§16. Каноническое распределение Гиббса
- •§21*. Распределение Максвелла как следствие канонического распределения Гиббса
- •§23. Большое каноническое распределение
- •§25. Распределение Ферми-Дирака
- •§26. Распределение Бозе-Эйнштейна
§3. Микро- и макро- параметры системы.
Каждое состояние системы описывается
набором динамических переменных
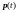 и
и
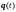 .
В ансамблях таких систем, из большого
числа параметров, которые можно построить
на переменных
и
,
можно выделить небольшое число параметров,
которые являются наиболее важными для
описания системы.
.
В ансамблях таких систем, из большого
числа параметров, которые можно построить
на переменных
и
,
можно выделить небольшое число параметров,
которые являются наиболее важными для
описания системы.
Введём такой параметр:
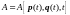
Выясняется, что эта величина в зависимости
от
 может принимать различные значения,
т.е. является функцией от
.
Параметр, определяемый динамическими
переменными называется микропараметром.
На ряду с этой величиной вводится
параметр аналогичный, который определяется
в более длительный момент времени и
характеризует систему в целом –
макропараметр.
может принимать различные значения,
т.е. является функцией от
.
Параметр, определяемый динамическими
переменными называется микропараметром.
На ряду с этой величиной вводится
параметр аналогичный, который определяется
в более длительный момент времени и
характеризует систему в целом –
макропараметр.
Будем рассматривать в этом курсе стационарные явления или стационарные системы - системы, свойства которых не зависят от времени. То есть, если рассмотреть ось , то для стационарных сред начало наблюдения за системой можно выбрать в любой точке оси :


И для таких процессов начальные условия динамических переменных не оказывают влияние на результат, т.е. начальные условия могут быть отброшены, так как часы пускаем в любой момент времени.
Итак, в стационарных системах:
время начала отсчёта
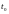 можно перемещать по оси времени.
можно перемещать по оси времени.начальные условия выкидываются
граничные условия, оказывается, не влияют на систему (если система стационарная).
Через границу вешнее воздействие проникает и через некоторое время действует на систему. Действие идёт через точки, находящиеся в очень узком приграничном слое. Т.к. количество этих точек мало, по сравнению с точками системы, то граничные условия можно не учитывать. Это обстоятельство можно использовать при рассмотрении двух подсистем. Взаимодействие подсистем в достаточно малом промежутке времени не оказывает влияние на подсистемы, так как на границе точек пренебрежимо мало по сравнению с подсистемами.
Выясняется, что микро и макро параметры
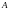 ,
если наблюдать за ними в течение большого
промежутка времени, то в большей части
этого промежутка времени, система
обладает конкретными или близкими к
нему параметрами. Если усреднить этот
параметр, то он не будет отличаться от
конкретного параметра.
,
если наблюдать за ними в течение большого
промежутка времени, то в большей части
этого промежутка времени, система
обладает конкретными или близкими к
нему параметрами. Если усреднить этот
параметр, то он не будет отличаться от
конкретного параметра.
В качестве результата наблюдения , принимается значение среднего по времени от :
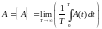
Если
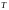 - время наблюдения, то выражение, стоящее
в скобках верно, но т.к.
очень велико, то пишут предел. Это и
предлагают воспринимать как наблюдаемую
величину (в теории).
- время наблюдения, то выражение, стоящее
в скобках верно, но т.к.
очень велико, то пишут предел. Это и
предлагают воспринимать как наблюдаемую
величину (в теории).
.
§4. Свойство эргодичности системы.
Итак, мы рассматриваем такие функции:
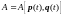
Параметр
испытывает флуктуации – отклонения от
некоторого среднего значения в течение
времени. На ряду с зависимостью
от
можно ввести характеристику – вероятность
того, что
лежит в интервале
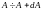 :
:
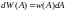
Как получить эту вероятность? Очевидно, если у нас стоит:
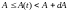
то
мы можем посчитать сумму всех промежутков
времени
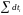 ,
в течение которых
,
в течение которых
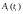 попадает этот интервал.
попадает этот интервал.
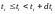
То есть мы подсчитываем длительность пребывания в слое .
О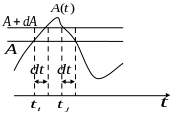 казывается,
что если все
казывается,
что если все
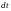 одинаковые, то
одинаковые, то
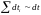 .
Так же оказывается, что
.
Так же оказывается, что
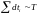 ,
где
- время наблюдения.
,
где
- время наблюдения.
Тогда:
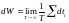 (*)
(*)
Это
вероятность того, что случайная величина
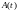 лежит
в пределах
лежит
в пределах
Плотность вероятности:
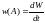
Здесь - это не случайная величина, а параметр. Случайной величиной является . С помощью (*) мы можем найти среднее по времени значение наблюдаемой величины.
