
- •§1. Экспериментальные основы квантовой механики
- •§2. Классическое и квантовое описание системы
- •[§3.] Принцип неопределенности
- •[§4.] Полный набор динамических переменных
- •[§5.] Постулаты квантовой механики
- •§6. Роль классической механики в квантовой механике
- •[§7.] Волновая функция и ее свойства
- •[§8.] Принцип суперпозиции состояний
- •§12. Среднее значение измеряемой величины
- •§13. Вероятность результатов измерения
- •[§15.] Операторы координаты , импульса , момента импульса , энергии .
- •[§ 19.] Волновое уравнение
- •[§ 24.] Оператор Гамильтона различных систем
- •§ 25. Стационарное состояние различных систем
- •[§ 28.] Собственный механический момент (спин)
- •§1. Статистическое описание систем с большим числом степеней свободы
- •§3. Микро- и макро- параметры системы.
- •§4. Свойство эргодичности системы.
- •§5. Два способа усреднения в статистической физике
- •§6. Понятие ансамбля систем
- •§7. Эргодическая гипотеза
- •§8. Равновесное состояние системы
- •§10. Квазизамкнутость и статистическая независимость подсистем
- •§15. Микроканоническое распределение Гиббса
- •§16. Каноническое распределение Гиббса
- •§21*. Распределение Максвелла как следствие канонического распределения Гиббса
- •§23. Большое каноническое распределение
- •§25. Распределение Ферми-Дирака
- •§26. Распределение Бозе-Эйнштейна
§6. Роль классической механики в квантовой механике
Два момента присутствия классической механики в квантовой механике:
Измерение микросистем (квантово-механических систем) проводятся с помощью классических приборов (систем).
Принцип соответствия – переход квантово-механических результатов в классическую механику ( 0, можно ввести такую величину размерности действия A, что
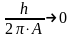 ).
По Эйнштейну этот переход характеризуется
).
По Эйнштейну этот переход характеризуется
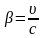 .
Если
.
Если
 ,
то переход в классическую механику
Ньютона.
,
то переход в классическую механику
Ньютона.
[§7.] Волновая функция и ее свойства
Волновая функция динамических переменных и времени определяет состояние системы с точностью до фазового множителя, т. е.
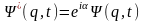
т. е.
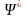 и
описывает
одно и тоже состояние, где
и
описывает
одно и тоже состояние, где
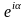 - фазовый множитель. Волновая функция
– комплексная, непрерывная, конечная.
У нее почти всюду существует конечная
производная по координате, но в некоторых
точках может терпеть скачек (особые
точки). Функции
-
нормируемые, т.е. квадратично интегрируемы.
Но для свободной материальной точки
не
нормируема.
- фазовый множитель. Волновая функция
– комплексная, непрерывная, конечная.
У нее почти всюду существует конечная
производная по координате, но в некоторых
точках может терпеть скачек (особые
точки). Функции
-
нормируемые, т.е. квадратично интегрируемы.
Но для свободной материальной точки
не
нормируема.
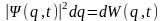
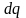 -
элементарный объем
-
элементарный объем
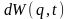 -
вероятность того, что динамические
переменные
лежат в интервале
-
вероятность того, что динамические
переменные
лежат в интервале
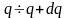 .
Это определение справедливо для
квадратично интегрируемых функций. Для
не квадратично интегрируемых функций
величина
.
Это определение справедливо для
квадратично интегрируемых функций. Для
не квадратично интегрируемых функций
величина
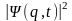 пропорциональна плотности вероятности.
пропорциональна плотности вероятности.
[§8.] Принцип суперпозиции состояний
Если мы имеем состояния системы,
описываемые функциями
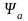 ,
то суперпозиции этих функций также
отвечает некоторое состояние этой
системы:
,
то суперпозиции этих функций также
отвечает некоторое состояние этой
системы:
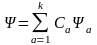
Отсюда получаем: уравнения, которым подчиняется функция должны быть линейными. Этот же вывод распространяется и на операторы в квантовой механике. Принцип суперпозиции требует использования в квантовой механике линейных операторов.
§12. Среднее значение измеряемой величины
По определению
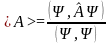 (12.1)
(12.1)
Рассмотрим
оператор
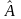 с дискретным спектром. Разложим
по собственным функциям оператора
:
с дискретным спектром. Разложим
по собственным функциям оператора
:
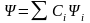 (12.2)
(12.2)
По
равенству Парсеваля
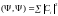 .
.
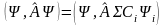
Т.к. оператор линейный, то его можно занести под знак суммы:
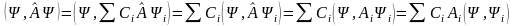
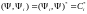
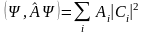 (12.3)
(12.3)
Подставляя (12.3) в числитель, а (12.2) в знаменатель для (12.1), имеем

Из
теории вероятности
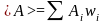 ,
где
,
где
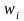 - вероятность получения
- вероятность получения
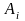 ,
тогда
,
тогда
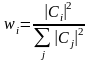
§13. Вероятность результатов измерения
Пусть
- вероятность того, что при измерении
величины
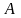 для системы, находящейся в состоянии
мы получим результат
.
Если система находится в состоянии
,
то величина
при измерении выходит с вероятностью
равной 1:
для системы, находящейся в состоянии
мы получим результат
.
Если система находится в состоянии
,
то величина
при измерении выходит с вероятностью
равной 1:
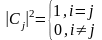
В общем случае;
Если полная производная оператора удовлетворяет равенству
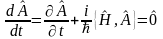 ,
,
то собственная функция оператора описывает состояние системы.
Для непрерывного спектра, вероятность
того, что результаты измерения величины
A для системы, находящейся
в состоянии
,
лежит в интервале от
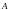 до
до
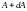 ,
определяется следующим выражением:
,
определяется следующим выражением:
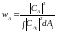 ,
,
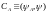 (13.1)
(13.1)
или
плотность вероятности

