Содержание:
1.Основные понятия теории алгоритмов.
2.Примитивно рекурсивные функции. Базис элементарных функций. Операции подстановки и примитивной рекурсии.
3.Примитивно рекурсивные функции. Основные свойства операций подстановки и примитивной рекурсии.
4.Примитивно рекурсивные функции относительно совокупности функций. Основные свойства.
14. Машина Тьюринга (МТ). Применение МТ к словам
16. Вычислимые по Тьюрингу функции.
17. Правильная вычислимость функций на машине Тьюринга.
18. Вычислимость по Тьюрингу примитивно рекурсивных функций. Суперпозиция.
19. Вычислимость по Тьюрингу примитивно рекурсивных функций. Примитивная рекурсия.
20. Вычислимость по Тьюрингу частично рекурсивных функций.
22. Нормальные алгоритмы Маркова и их применение к словам.
23. Нормально вычислимые функции и принцип нормализации Маркова.
15.Конструирование МТ. Операции над машинами Тьюринга.
1.Основные понятия теории алгоритмов.
под алгоритмом понимается – единый метод решения определенного класса однотипных задач, обладающий свойствами дискретности, определенности, массовости, результативности и оперирующий конструктивными объектами.
Дискретность:
Процесс построения величин, задаваемый алгоритмом, протекает в дискретном времени следующим образом: в начальный момент задается исходная конечная система величин, а в каждый следующий момент система величин, получается по определенному закону из системы величин, имевшихся в предыдущий момент времени.
Детерминированность (определенность)– система величин, получаемых в любой, отличный от начального, момент времени, однозначно определяется системой величин, полученных в предшествующие моменты времени.
Элементарность шагов – закон получения последующей системы величин из предшествующей должен быть простым и локальным.
Эффективность (результативность)– каждый шаг работы алгоритма должен заканчиваться результатом.
Массовость алгоритма – начальная система величин может выбираться из некоторого потенциально бесконечного счетного множества Х.
Конструктивность – объекты из Х, над которыми работает алгоритм, должны быть конструктивными.
Конструктивный объект –это такой объект, который может быть набран весь целиком и представлен нам для рассмотрения.
Конструктивные объекты
булевы функции
формулы алгебры логики
натуральные и рациональные числа
матрицы с натуральными или рациональными элементами
многочлены от неизвестных с рациональными коэффициентамии т.п.
Неконструктивные объекты
любые
действительные числа, представление
которых в десятичной записи
ни для какого n ϵ N
не может быть целиком представлено для
рассмотрения.
Например, число е и π не являются конструктивными объектами.
2.Примитивно рекурсивные функции. Базис элементарных функций. Операции подстановки и примитивной рекурсии.
Теория рекурсивных функций включает следующие классы функций: класс примитивной рекурсивной функции (ПРФ), класс общерекурсивной функции (ОРФ) и класс частично рекурсивной функции (ЧРФ).
Образование теории рекурсивных функций:
задается базис элементарных функций,
определяются специальные операции над функциями,
В результате применения определенного количества операций к элементарным функциям, строятся соответствующие классы функций: класс ПРФ, ОРФ и ЧРФ.
Примитивно рекурсивные функции (ПРФ)
Определение. Элементарными функциями называются:
1).
Функции константы
,
где n=0,1,2,…
q=0,1,2,….
2). Функции следования S(x)=x+1
3).
Функции выбора
,
где 1≤m≤n.
Все элементарные функции - всюду определенные и алгоритмически вычислимые.
Имеется небольшое число операций над элементарными функциями, переводящими вычислимые функции снова в вычислимые.
Операция подстановки
Пусть
задана функция
и функции
.
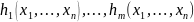Определение.
Говорят,
что функция f
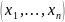получена из этих функций с применением
операции подстановки, если выполняется
следующее равенство:
f
.
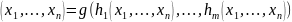и
обозначается f=S(g,,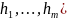
где S–означает
операции подстановки.
Операция примитивной рекурсии
Пусть
задана функция g
и функция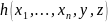
.
Определение.
Говорят, что функция
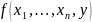получена из функциий g
и
с помощью операции примитивной рекурсии,
если выполняются следующие равенства:
.
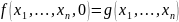
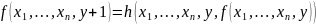Это
опред-е имеет смысл, когда n≠0,
при этом запис-ся: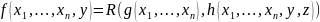
или сокращенно, f=R(g,h), где R–означает операцию примитивной рекурсии.
В
случае, когда n=0
операция примитивной рекурсии примет
вид: φ(0)=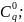
,
и
обозначается:φ=R(