9.Непрерывные случ. Вел-ны

Опр.1 Случ. вел-на Х наз-ся непрерывной, если её ф-ия распределения F(X) непрерывна в любой точке числовой прямой и диф-ма всюду, кроме, быть может, отдельных точек, где она терпит излом.

Опр.2. Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: f(x) = F'(x).

Свойства:

Свойство 1. Плотность распределения неотрицательна, т.е. f(x) ≥ 0. (как производная неубывающей ф-ии распределения)

Свойство 2. Вер-ть попадания непрер-ой случ. вел-ны в 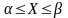равна

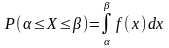
Док-во: 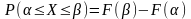. Но т.к ф-я распред-я явл-ся первообразной для плотности (по опред.), то по ф-ле Ньютона-Лейбница, приращ-е первообразной на отрезке – это и есть опред-ый интеграл.

Свойство 3. Ф-ия распределения непрер-ой случ. вел-ны равна F(x) = ∫^х_–∞ f(x)∙dx. Док-во: F(X)=P{X<x}=P{– <X<x} и по св-ву 2 следует св-во 3.

Свойство 4. Несобственный интеграл от плотности распределения в пределах от -∞ до +∞ равен единице: ∫^+∞_-∞ f(x)∙dx = 1. Док-во: рассм-м

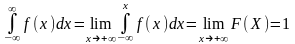
10.Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством: M(x) = ∫^+∞_-∞ x∙f(x)∙dx, где f(x) – плотность распределения случайной величины Х. Предполагается, что интеграл сходится абсолютно.

Все свойства математического ожидания, указанные для дискретных случайных величин, сохраняются и для непрерывных величин.

Опр.4. Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством: D(x) = ∫^+∞_-∞ [x – M(x)]²∙f(x)∙dx, или равносильным равенством: D(x) = ∫^+∞_-∞ x²∙f(x)∙dx – [M(x)]².

Все свойства дисперсии, указанные для дискретных случайных величин, сохраняются и для непрерывных величин.

11. Опр.5. Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной величины: σ(х) = √D(x).

Опр.6. Модой М₀(Х) непрерывной случайной величины Х называют то её возможное значение, которому соответствует локальный максимум плотности распределения. В частности, если распределение имеет два одинаковых максимума, то его называют бимодальным.

Опр.7. Квантиль порядка р есть точка (число) х_р такая, что вероятность попадания случайной величины левее этой точки, равна р: Р(Х < x_p) = p.

Квантиль порядка 1/2 называется медианой.

Опр.8. Медианой М_е(Х) непрерывной случайной величины Х называют то её возможное значение, которое определяется равенством: Р[X < М_е(Х)] = P [ X > М_е(Х)].

Геометрически медиану можно истолковать как точку, в которой ордината f(x) делит пополам площадь, ограниченную кривой распределения.

12. Начальный теоретический момент порядка k непрерывной случайной величины Х определяется равенством: ν_k = ∫^+∞_-∞ x^k∙f(x)∙dx.

Опр.10. Центральный теоретический момент порядка k непрерывной случайной величины Х определяется равенством: µ_k = ∫^+∞_-∞ [x – M(x)]^k∙f(x)∙dx.

Центральные моменты выражаются через начальные моменты по формулам: μ₂ = ν ₂ – ν ²₁, μ₃ = ν ₃ – 3 ν ₁ ν ₂ + 2 ν ³₁, μ₄ = ν ₄ – 4 ν ₁ ν ₃ + 6 ν ²₁ ν ₂ – 3 ν ⁴₁.

13.Биномиальным называют закон распределения дискретной случайной величины Х – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна р; вероятность возможного значения Х = k (числа k появлений события) вычисляются по формуле Бернулли: P_n(k) = C^k_n p^k q^n-k.

Или другими словами: при повторении n одинаковых независимых опытов некоторое событие А может случиться k раз. Если каждый раз вероятность результата А есть р, то случайная величина имеет биномиальное распределение.

Опр.3. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании: M(X) = np.

Опр.4. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X) = npq.

14Биномиальный закон распред Если число испытаний велико (n >> 1), а вероятность р появления события в каждом испытании очень мала (p << 1), то используют приближённую формулу: P_n(k) = λ^k e^-λ / k!, где k – число появлений события в n независимых испытаниях, λ = np (среднее число появлений события в n испытаниях), и говорят, что случайная величина распределена по закону Пуассона.

Опр.6. Математическое ожидание распределения Пуассона равно произведению числа испытаний на вероятность появления события в одном испытании: M(X) = np = λ.

Опр.7. Дисперсия распределения Пуассона равна произведению числа испытаний на вероятность появления события в одном испытании, то есть равна математическому ожиданию: D(X) = np = λ.

Теорема Пуассона: Если число опытов n велико, а вер-ть успеха в отдельном опыте р мала (0<p<1) и произведение np= λ = const, то ф-лу Пуассона с параметром λ =.np м приблизительно применять вместо ф-лы Бернулли: P_n(m) = C^m_np^mq^n­–m причём k=0,1,…n,..

Замечание: использование ф-лы Пуассона как предельной для ф-лы Бернулли оправдывает себя при npq 9