
- •3. Геометрическая вероятность.
- •7. Закон распределения и функц. Распред. Дискретной случ. Величины
- •9.Непрерывные случ. Вел-ны
- •Показательный закон распределения
- •22. Основные понятия теории оценок
- •24. Методы получения оценок: метод моментов и метод наибольшего правдоподобия, функция правдоподобия( дискретный и непрерывный случаи), примеры.
- •26.Общая схема проверки гипотез:
1 Перестановки: Pn = n! , n! = 1∙2∙3∙…∙n. отличаются только порядком их расположения
Размещение: Amn = n!/(n-m)! = n(n–1)(n–2)…(n–m+1). отличаются либо составом элементов, либо их порядком (Порядок важен)
Сочетание: Cmn = n! / (m! (n-m)!). отличаются хотя бы одним элементом (Порядок не важен)
Amn = Pm ∙ Cmn
Перестановки с повторением: Pn (n1, n2, …) = n! / (n1! n2! …),где n1 + n2 + … = n.
2.Классическое опр. вероятностей Элем-ные соб-ия, при кот-х данное интересующее нас событие наступает, наз-ся благоприятными.
Для полной группы равновозможных и попарнонесовместных событий вер-ть соб. А наз-ся отношение числа m благоприятных элементарных событий к общему числу всех возможных элем-ных событий n в данном опыте P(A) = m / n
Классическая вероятность: элементарный исход, события, конечная схема, определения, примеры. Вероятность и частота.
Определение вероятности
Пусть некоторый эксперимент имеет N элементарных исходов. Будем считать, что исходы не совместны, т.е. в результате конкретного эксперимента происходит только 1 элемент. исход. Элемент. исходы равновозможны. Тогда припишем каждому элементарному исходу число 1/N. Любое подмножество множества Ω = {w1,…wN}. Всякое элементарное событие содержится в некотором событии А назовем благоприятным событию А.
Определение
Пусть m — число элементарных исходов, благоприятных событию А. Тогда классич. вероятность события А = m/N. Обозначается как Р(А) = m/N.
Пример1
Игральная кость. Найти вероятность того, что выпадет 5 или 6.
Событие А = {5 или 6}
N = 6
Р(А) = 1/3 (2 из 6-ти возможных).
Относительная частота события А определяется равенством W(A) = m/n, где m — число испытаний, в которых событие А наступило, а n — общее число произведенных испытаний.
Вероятность и частота.
Статистический подход.
Проводим эксперимент n раз и фиксируем, произошло или нет в рез-те событие А. Пусть оно произошло k раз, тогда k/n – частота события А (для больших n близко к постоянной величине). Если отклонение k/n от этой постоянной величины с ростом n уменьшается,- устойчивость частот. Впервые это заметили, изучая демографические вопросы: % смертности в опред. возрасте для опред-х групп населения. Были попытки построить теорию, принимая за вероятность частоту события, но возникли сложности.
3. Геометрическая вероятность.
Постановка задачи: пусть G – огранич. плоская область с конечной площадью. В эт. области содержится обл. g облад-щая те-ми же св-ми. В обл. G наугад бросается точка, она может попасть в любое место обл-ти G (рис.1). Вер-ть точки попасть в g пропорциональна отношению площадей G и g и не зависит от ее формы и расположения. Т.о. вер-ть попадан. в обл. g точки, брош. в обл. G наудачу, =, по опред.: Р=S(g)/S(G), S(g) и S(G) – площ. g и G в общем виде S(g) и S(G) – меры множеств g и G.
Задача о встрече: Два лица А и В условились встретиться м/у 12 и часом дня. Пришедший первым ждёт 20 минут и уходит. Какова вероятность встречи, если приход каждого в течен. часа мож. произойти наудачу и моменты прихода А и В независимы. Решение: обозначим момент прихода А через х, а В – у. Изобразим х и у как декарт. коорд-ты, единиц. масшт. – 1 мин. (рис.2). Всевозможн. исходы можн. изобразить ввиде пар (х, у) – т. квадрата со стороной 60. Встр. состоится, если x – y ≤20 (заштрих. обл.). Область G =60 2, g = 60 2 - 2*0,5*(40*40) = 602- 402, p = (602- 402) / 602= 5 / 9.
4. Теоремы сложения и умножения вер-тей
Теорема сложения
вер-тей:
Вер-ть суммы
2-х совместных соб-ий = вер-ти суммы этих
событий минус вер-ть их пересечений
АВ
![]() => P(A+B)=P(A)+P(B)-P(AB)
=> P(A+B)=P(A)+P(B)-P(AB)
Док-во: А+В=А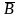 +AB+B
+AB+B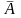
А
,
AB,
B
–![]() попарно несовместны =>
Р(А+В)=Р(А
)+Р(В
)+Р(АВ).
попарно несовместны =>
Р(А+В)=Р(А
)+Р(В
)+Р(АВ).
Выразим через А,В,АВ:
А= А +АВ
B=B +AB
Р(А)=Р(А +АВ)
Р(В)= B +AB =>
Р(B )=P(B)–P(AB)
P(А )=P(A)–P(AB)
подставляем в Р(А+В): Р(А+В)= P(A)–P(AB)+P(B)–P(AB)+Р(АВ)= P(A)–P(AB)+P(B). Теорема доказана
Теорема умножения вероятностей: Вер-ть совместного появления двух событий равна произведению вер-ти одного из них на условную вер-ть другого, вычисленную в предположении, что первое событие уже наступило:P(AB) = P(A) ∙ PA(B).Для независимых событий:P(AB) = P(A) ∙ P(B), т.е. вер-ть совместного появления двух независимых событий равна произведению вер-тей этих событий.
5. Формула полной вероятности: Вер-ть события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) В1, В2, … , Вn, образующих полную группу, равна сумме произведений вер-тей каждой из гипотез на соответствующую условную вер-ть события А:P(A) = P(B1) ∙ PB1(A) + P(B2) ∙ PB2(A) + … + P(Bn) ∙ PBn(A), где P(B1) + P(B2) + … + P(Bn) = 1.
Формула Бейеса: Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) В1, В2, … , Вn, которые образуют полную группу событий. Если событие А уже произошло, то вер-ти гипотез могут быть переоценены по формулам Бейеса: PA(Bi) = P(Bi) ∙ PB1(A) / P(A) (i = 1, 2, … , n), где P(A) = P(B1) ∙ PB1(A) + P(B2) ∙ PB2(A) + … + P(Bn) ∙ PBn(A).
6. Формула Бернулли: Pn(m) = Cmnpmqn–m, где n – число опытов в одинаковых условиях, m – число опытов, в которых произошло событие А, р – вероятность события А при каждом испытании, q = 1 – p.
Функция распределения: F(x) = P(X < x) = ∑ xi<x p(xi).
