Раздел «Химическая кинетика. Катализ»

Пример 11

Для некоторой реакции, протекающей по первому порядку n = 1, даны значения констант скоростей k при различных температурах

Таблица 7

Т, К	556	629	666	700	784
k, с-1	3,52 · 10-7	3,02 · 10-5	2,19 · 10-4	1,16 · 10-3	3,95 · 10-2

11.1. Постройте графики зависимости k = f(Т) и lnk = f ;

11.2. Вычислите энергию активации этой реакции графически и аналитически.

Р е ш е н и е

11.1. Для построения графиков по данным табл. 7 (рис. 7, 8) выразим величины k с одинаковым множителем 10^-4, посчитаем lnk и , полученные значения сведем в табл. 8.

11.2. Для определения энергии активации Е используем уравнение Аррениуса в интегральной логарифмической форме [2, с. 316].

Таблица 8

Т, К	k, с-1	, К-1	lnk
556	0,0035 · 10-4	1,8 · 10-3	-14,85
629	0,302 · 10-4	1,59 · 10-3	-10,41
666	2,19 · 10-4	1,50 · 10-3	-8,42
700	11,6 · 10-4	1,43 · 10-3	-6,76
784	395 · 10-4	1,21 · 10-3	-3,23

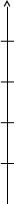k · 10⁴, c^-1

400

300

200

100

Т,К

500 600 700 800

Рис. 7. График зависимости k = f(T)

Для графического определения Е используем уравнение в виде:

,

окуда вытекает, что на графике в координатах lnk = f (рис. 8), тангенс угла наклона прямой .

Из графика находим, что tg = .

lnk

- 5

а

- 10

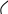
в  

- 15

1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 · 10³, К^-1

Рис. 8. График зависимости lnk = f

, откуда Е = tg · R = 23200 · 8,314 = 192884 Дж = 192,9 кДж.

Для аналитического определения Е используем данные табл. 7 и уравнение:

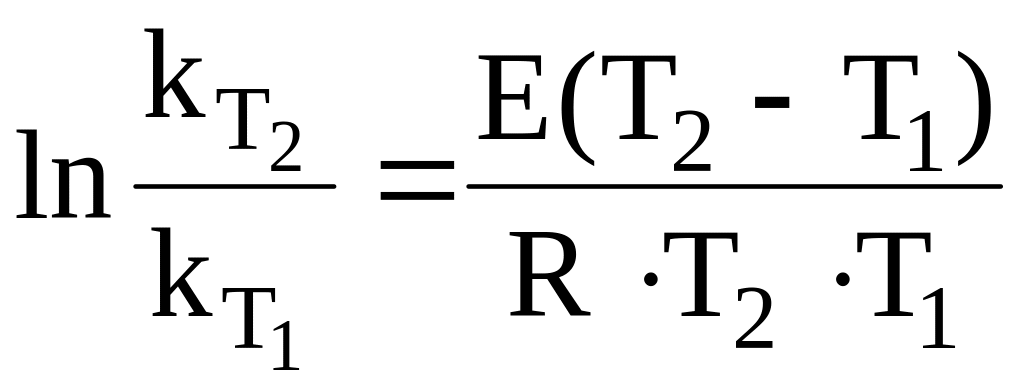, откуда

;

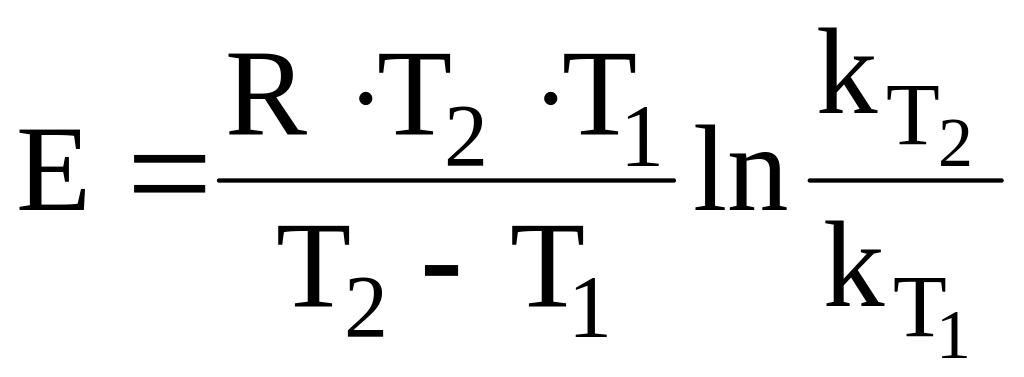1. Т₁ = 556 К; = 3,52 · 10^-7 с^-1;

Т₂ = 666 К; = 2,19 · 10^-4 с^-1;

.

2. Т₁ = 629 К; = 3,02 · 10^-5 с^-1;

Т₂ = 784 К; = 3,95 · 10^-2 с^-1;

.

3. Т₁ = 700 К; = 1,16 · 10^-3;

Т₂ = 784 К; = 3,95 · 10^-2;

.

Находим среднее значение энергии активации:

187,2 кДж.

Энергии активации, вычисленные графически и аналитически, практически одинаковы.

Пример 12

Для реакции 2NO₂  N₂ + 2O₂

по значениям констант при двух температурах

Т₁ = 986 К; k₁ = 6,72 л·моль^-1·мин^-1.

Т₂ = 1165 К; k₂ = 977 л·моль^-1·мин^-1.

Определите

12.1. Энергию активации;

12.2. Константу скорости при Т₃ = 1053 К;

12.3. Температурный коэффициент скорости реакции ;

12.4. Количество вещества, прореагировавшее при Т₁ = 986 К за время t = 65 мин, если начальная концентрация С⁰ = 1,75 моль/л.

Примите порядок реакции равным молекулярности n = 2.

Р е ш е н и е

12.1. Энергию активации выражаем из интегральной логарифмической формы уравнения Аррениуса [2, с. 316]:

.

12.2. Величину константы скорости k₃ при температуре Т₃ = 1053 К также выражаем из уравнения Аррениуса

;

;

K₃ = е^3,967 = 52,83 л · моль^-1 · мин^-1.

12.3. Температурный коэффициент скорости реакции  выражаем из правила Вант-Гоффа [2, с. 314]:

; ;

,

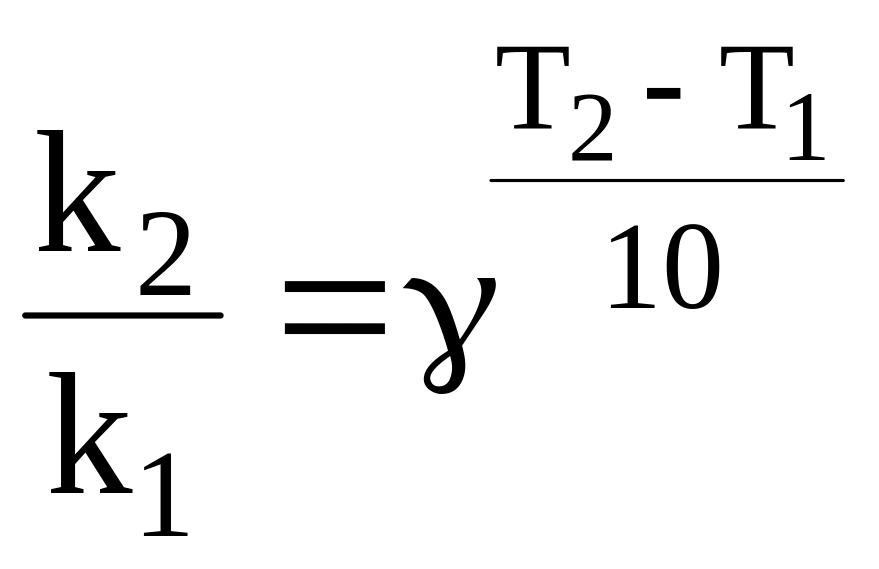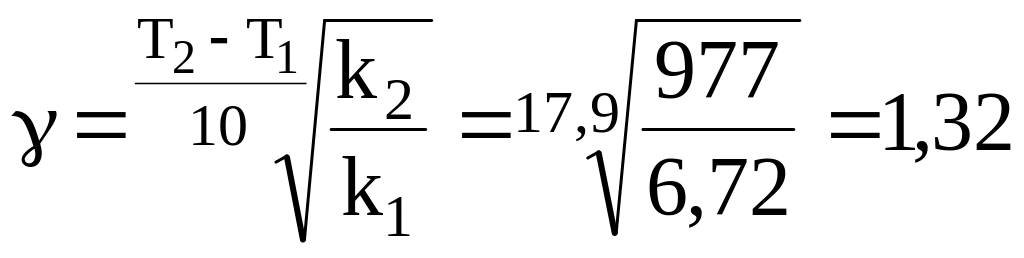где .

Величина температурного коэффициента меньше, чем по правилу Вант-Гоффа ( = 2  4).

12.4. Для реакции второго порядка [2, с. 302]

,

где х – количество вещества, прореагировавшее за время реакции t;

С⁰ – начальная концентрация исходного вещества.

Откуда выражаем величину х:

.

По условию задачи k = 6,72 л · моль^-1 · мин^-1 при Т = 986 К; t = 65 мин; С⁰ = 1,75 моль/л.

Находим .

За 65 мин вещество NO₂ практически полностью разложится при Т = 986 К.

Если порядок реакции первый n = 1, то для определения количества х, прореагировавшего за время реакции t следует воспользоваться кинетическим уравнением реакции первого порядка [2, с. 301]:

.