Раздел «Электрохимия»

Пример 7

Дана зависимость удельного сопротивления водных растворов HNO₂ и СН₃СООК от концентрации (табл. 5).

Таблица 5

Концентрация С, кмоль/м3	Удельное сопротивление r, Ом · м
	HNO2	СН3СООК
0,1	4,32	1,035
0,05	5,70	1,970
0,01	13,40	9,220
0,005	20,40	18,200
0,001	52,70	87,600

7.1. Постройте графики удельной æ и молярной l электрических проводимостей растворов HNO₂ и СН₃СООК от концентрации С.

7.2. Рассчитайте константу диссоциации и проверьте, подчиняются ли растворы HNO₂ и СН₃СООК в воде закону разведения Оствальда.

7.3. Определите для HNO₂ и СН₃СООК по данным зависимости молярной электрической проводимости l от концентрации С молярную электрическую проводимость при бесконечном разведении l_¥ и сопоставьте экспериментальные величины со справочными, рассчитанными по предельным электрическим проводимостям ионов.

Р е ш е н и е

Для построения графиков необходимо рассчитать по исходным данным (табл. 5) величины удельной электрической проводимости æ и молярной электрической проводимости l по формулам [2, с. 235, 236]:

æ ; .

Для измерения æ и l используем единицы СN.

Множитель 1000 при расчете l учитывает перевод концентрации С, в киломолях на кубический метр в С в молях на кубический метр.

Для определения константы диссоциации электролита К_д по закону разведения Оствальда необходимо определить величину степени диссоциации электролита :

; .

Предельную молярную электрическую проводимость l_¥ для каждого электролита рассчитаем по справочным значениям предельных молярных электрических проводимостей ионов (приложение, табл. V или [11]).

l_¥(HNO₂) = l_¥(Н⁺) + l_¥(NO₂^-) = 349,8 · 10^-4 + 72,0 · 10^-4 = = 421,8 · 10^-4 Ом^-1 · м² · моль^-1.

l_¥(СН₃СООК) = l_¥(К⁺) + l_¥(СН₃СОО^-) = 40,09 · 10^-4 + 73,5 · 10^-4 = = 113,6 · 10^-4 Ом^-1 · м² · моль^-1.

Приведем расчеты æ, l, a и К_д для HNO₂ и СН₃СООК для концентрации С = 0,1 кмоль/м³ по данным табл. 5.

HNO₂

æ = = 0,231 Ом^-1 · м^-1; l = = 23,2 · 10^-4 Ом^-1 · м² · моль^-1; ; ;

СН₃СООК

æ = = 0,966 Ом^-1 · м^-1; l = = 96,6 · 10^-4 Ом^-1 · м² · моль^-1; ; .

Для остальных концентраций (табл. 5) все величины рассчитаем и запишем в табл. 6.

Таблица 6

Вещество	С, кмоль/м3	æ, Ом-1 · м-1	l, Ом-1 · м2 · моль-1	a	Кд
	0,1	0,231	23,2 · 10-4	0,055	3,2 · 10-4
HNO2	0,05	0,175	35,0 · 10-4	0,083	3,76 · 10-4
	0,01	0,0746	74,6 · 10-4	0,177	3,78 · 10-4
	0,005	0,0490	98,0 · 10-4	0,232	3,50 · 10-4
	0,001	0,0190	190 · 10-4	0,450	3,68 · 10-4
СН3СООК	0,1	0,966	96,6 · 10-4	0,847	0,47
	0,05	0,508	101,6 · 10-4	0,888	0,35
	0,01	0,108	108,0 · 10-4	0,944	0,16
	0,005	0,055	110,0 · 10-4	0,962	0,12
	0,001	0,011	110,0 · 10-4	0,962	0,12

Из графиков æ = f(С) и l = f(С) (рис. 6) следует, что с увеличением концентрации удельная электрическая проводимость æ HNO₂ и СН₃СООК увеличивается, а молярная электрическая проводимость l уменьшается.

Для HNO₂ константы диссоциации практически не изменяются с увеличением концентрации (табл. 6), следовательно, раствор HNO₂ подчиняется закону разведения Оствальда, HNO₂ является слабым электролитом.

Для СН₃СООК константы диссоциации изменяются с изменением концентрации (табл. 6), раствор СН₃СООК не подчиняются закону разведения Оствальда, СН₃СООК – сильный электролит.

Для определения экспериментальных значений предельных электрических проводимостей l_¥(HNO₂) и l_¥(СН₃СООК) проэкстраполируем зависимости l = f(С) (рис. 6) к нулевому значению концентрации:

l_¥(HNO₂) » 230 · 10^-4 Ом^-1 · м² · моль^-1;

l_¥(СН₃СООК) = 112 · 10^-4 Ом^-4 · м² · моль^-1.

Для HNO₂ определенная по графику (рис. 6) величина l_¥ плохо согласуется со справочной (421,8 · 10^-4 Ом^-1 · м² · моль^-1).

Для СН₃СООК определенная по графику (рис. 6) величина l_¥ хорошо согласуется со справочной (113,6 · 10^-4 Ом^-4 · м² · моль^-1).

Пример 8

Для окислительно-восстановительного элемента Pt|A,B||C,D|Pt, составленного из электродов Pt|H₃AsO₄, HAsO₂, H⁺ и Pt|Cr³⁺, Cr²⁺ при следующих активностях окисленной и восстановленной форм веществ:

а(H₃AsO₄) = 0,06; а(HAsO₂) = 0,02; а(Cr³⁺) = 0,025; а(Cr²⁺) = 0,45.

8.1. Запишите стандартные электродные потенциалы и определите, какой электрод является отрицательным (анодом), а какой – положительным (катодом); напишите схему гальванического окислительно-восстановительного элемента.

8.2. Напишите электронные уравнения процессов, протекающих на каждом электроде, и суммарное уравнение реакции, протекающей в окислительно-восстановительном элементе.

8.3. Вычислите стандартную электродвижущую силу ЭДС элемента и константу химического равновесия.

8.4. Вычислите ЭДС элемента при Т = 298 К, соответствующую заданным активностям окисленной и восстановленной форм веществ. Примите = 1; =0,2.

æ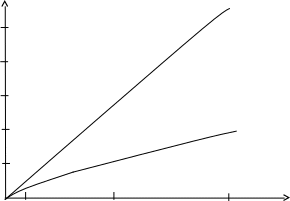 , Ом^-1·м^-1 СН₃СООК

а

1,0

0,8

0,6

0,4

HNO₂

0,2

0

0,01 0,05 0,1 С, кмоль/м³

 · 10⁴,

О м^-1·м²

· моль^-1 200

б

160

120

СН₃СООК

80

40

HNO₂

0

0,01 0,05 0,1 С, кмоль/м³

Рис. 6. Графики зависимостей удельной (а) и молярной (б) электрических

проводимостей от концентрации для HNO₂ и СН₃СООК

Р е ш е н и е

8.1. Из справочной табл. VI (приложение или [11, 12]) выпишем значения стандартных электродных потенциалов Е⁰ для электродов:

Pt|H₃AsO₄, HAsO₂, H⁺; Е⁰ = +0,560 В;

Pt|Cr³⁺, Cr²⁺; Е⁰ = –0,408 В.

Отрицательным электродом (анодом) в элементе будет электрод Pt|Cr³⁺, Cr²⁺, так как он имеет меньшее значение электродного потенциала, а электрод Pt|H₃AsO₄, HAsO₂, H⁺ будет катодом.

Составляем схему гальванического окислительно-восстановительного элемента:

А(-)Pt|Cr³⁺, Cr²⁺ || H₃AsO₄, HAsO₂, H⁺|Pt (+)К.

8.2. Запишем электронные уравнения процессов, протекающих на аноде и катоде, и суммарное уравнение реакции в элементе:

А(-): Cr2+ – ē = Cr3+	2	окисление
K(+): H3AsO4 + 2H+ + 2ē = HAsO2 + 2H2O	1	восстановление

2Cr²⁺ + H₃AsO₄ + 2H⁺ = 2Cr³⁺ + HAsO₂ + 2H₂O.

8.3. Рассчитаем стандартную ЭДС ⁰ как разность между стандартным электродным потенциалом положительного электрода (катода) и стандартным электродным потенциалом отрицательного электрода (анода) [2, с. 252]:

= 0,560 – (–0,408) = 0,968 В.

Константу равновесия рассчитаем по формуле, которая вытекает из соотношений: DG⁰ = –RTlnK [2, с. 112] и DG⁰ = –nF⁰ [2, с. 266]:

.

n = 2 (число электронов в окислительно-восстановительной реакции элемента); F = 96500 Кл/моль (число Фарадея).

Так как константа равновесия очень велика, реакция в элементе практически необратима и протекает в прямом направлении.

8.4. Рассчитаем равновесные электродные потенциалы, соответствующие заданным активностям, по уравнению Нернста [2, с. 258] при Т = 298 К:

,

где n – число электронов в электродной реакции;

Па₀, Па_R – произведение активностей окисленной и восстановленной форм веществ, соответственно.

= ;

= .

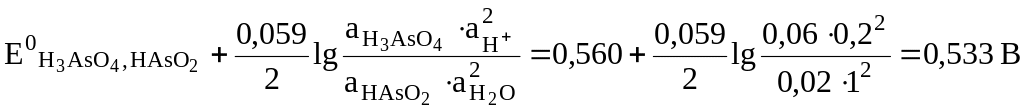Рассчитаем ЭДС элемента, соответствующую рассчитанным значениям равновесных потенциалов электродов:

 = 0,533 – (–0,482) = 1,015 В.

Пример 9

Для элемента, составленного из водородного электрода Н⁺|H₂,Pt (пластина насыщена водородом при давлении = 2,0 атм) в растворе электролита С:

Вариант 1. НСООН с концентрацией С_m = 0,1 моль/кг Н₂О;

Вариант 2. NaOH с концентрацией С_m = 0,1моль/кг Н₂О,

и каломельного электрода Hg, Hg₂Cl₂|Cl^- с концентрацией KCl С_m = = 0,5 моль/кг Н₂О.

9.1. Вычислите электродные потенциалы водородного и каломельного электродов.

9.2. Вычислите ЭДС элемента (диффузионную ЭДС примите равной нулю).

9.3. Вычислите рН раствора электролита С.

Р е ш е н и е

9.1. Рассчитаем потенциал каломельного электрода по уравнению Нернста [2, с. 259], приняв моляльную концентрацию KCl равной молярной, активности твердых фаз Hg и Hg₂Cl₂ равными единице, коэффициент активности KCl равным единице.

Электродная реакция, протекающая на каломельном электроде, и соответствующая величина стандартного электродного потенциала (приложение, табл. VI или [11, 12]):

½ Hg₂Cl₂ + ē = Hg + Cl^- ; .

Каломельный электрод относится к электродам второго рода, тогда, в соответствии с уравнением Нернста (Т = 298 К):

= ,

где ;

n = 1 (число электронов в электродной реакции).

.

Рассчитаем потенциал водородного электрода (Т = 298 К), который относится к газовым электродам, также по уравнению Нернста [2, с. 258].

Из табл. VI (приложение) или [11, 12] запишем электродную реакцию, протекающую на водородном электроде, и величину стандартного электродного потенциала.

Н⁺ + ē = ½ Н₂; = 0;

= ,

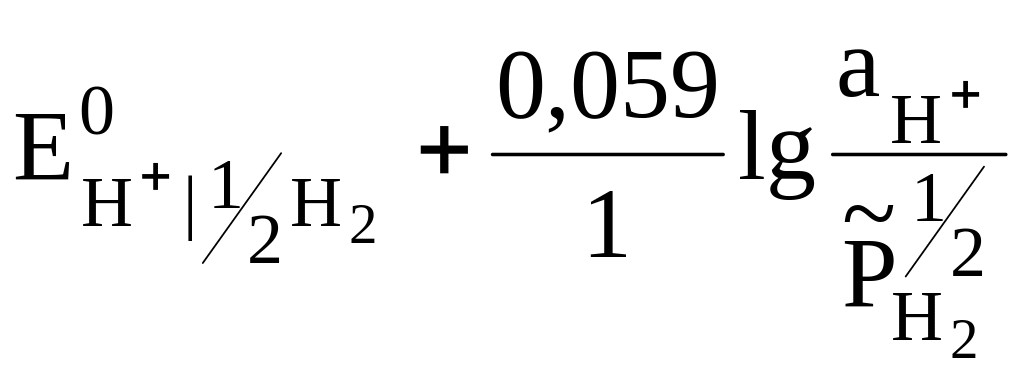где  активность катионов водорода;

 относительное парциальное давление водорода;

Если давление выражается в атмосферах, то:

.

Вариант 1

Электролит С – НСООН (слабая кислота), С_m = 0,1 моль/кг Н₂О; К_д = 1,772 · 10^-4 (прил., табл. VII или [9,10]).

В этом случае

.

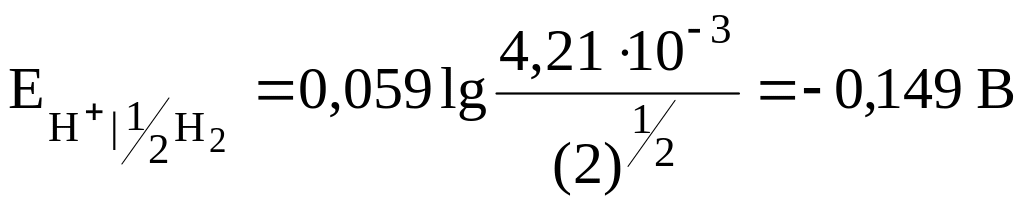Вариант 2

Электролит С – NaOH (сильный электролит), С_m = 0,1 моль/кг Н₂О.

Примем С_m(NaOH) = С_м(NaOH); (NaOH) = 1;

тогда = а(NaOH) = С_м(NaOH) · (NaOH) = 0,1 · 1 = 0,1.

Учитывая, что ионное произведение воды при 298К равно 1 · 10^-14:

;

.

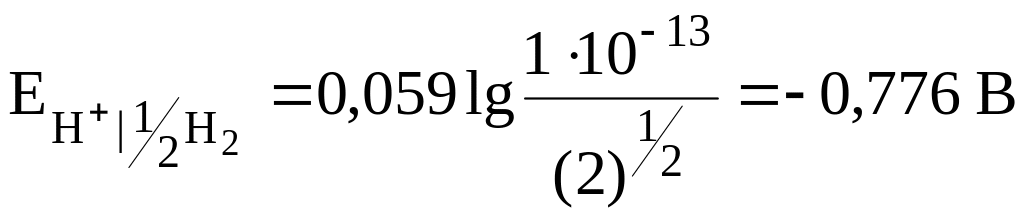9.2. Вычислим ЭДС  элемента, составленного из водородного и каломельного электродов:

А(-) Pt,H₂|H⁺ || Cl^-|Hg₂Cl₂, Hg (+)K,

в котором анодом (отрицательным) электродом является водородный электрод, так как меньшее значение электродного потенциала

;

Вариант 1

 = 0,285 – (-0,149) = 0,434 В;

Вариант 2

 = 0,285 – (-0,776) = 1,061 В.

9.3. Вычислим рН раствора электролита С

Вариант 1

Электролит НСООН, С_m = 0,1 моль/кг Н₂О

рН = -lg = -lg4,21 · 10^-3 = 2,38;

рН < 7, среда кислая;

Вариант 2

Электролит NaOH, С_m = 0,1 моль/кг Н₂О

рН = -lg1 · 10^-13 = 13;

рН > 7, среда щелочная.

Пример 10

Для реакции

2Ag + Hg₂Cl₂ = 2AgCl + 2Hg,

протекающей обратимо в гальваническом элементе, дано уравнение зависимости ЭДС от температуры:

 = 0,556 + 3,388 · 10^-4Т.

10.1. При температуре Т = 323 К вычислите ЭДС элемента и термодинамические параметры (G, H, S) реакции, протекающей в элементе.

10.2. По полученным значениям термодинамических функций охарактеризуйте реакцию, протекающую в элементе.

Р е ш е н и е

Для реакции 2Ag + Hg₂Cl₂ = 2AgCl + 2Hg число электронов, принимающих участие в токообразующей реакции, n = 2.

А(-): 2Ag – 2ē + 2Cl^- = 2AgCl

K(+): Hg₂Cl₂ + 2ē = 2Hg + 2Cl^-.

10.1. Рассчитаем ЭДС при 323 К по заданному уравнению:

 = 0,556 + 3,388 · 10^-4 · 323 = 0,665 В.

Изменение энергии Гиббса равно [2, с. 266]:

G = –nF,

где n – число электронов в токообразующей реакции;

F – число Фарадея (96500 Кл/моль).

G = –2 · 96500 · 0,665 = –128345 Дж = 128,3 кДж.

Изменение энтропии можно рассчитать, зная зависимость ЭДС от температуры [2, с. 266]:

,

где – температурный коэффициент ЭДС.

Для определения температурного коэффициента ЭДС продифференцируем по температуре уравнение зависимости  от Т

.

Тогда S = 2 · 96500 · 3,388 · 10^-4 = 65,39 Дж/К.

Изменение энтальпии можно выразить из известного соотношения:

G = H - TS, откуда

=

= –2 · 96500 (0,665 – 323 · 3,388 · 10^-4) = –107224,5 Дж = –107,2 кДж.

10.2. Охарактеризуем реакцию, протекающую в элементе:

G < 0, следовательно, при постоянных давлении и температуре реакция протекает самопроизвольно;

S > 0, реакция протекает с увеличением беспорядка в системе (система становится менее упорядоченной);

Н < 0, реакция протекает с выделением теплоты, т. е. является экзотермической.