27.Методы асинхронного и синхронного моделирования. Виды состязаний в цифровых схемах.
Схемы, подлежащие моделированию, обычно представляются в виде компонентов. Если компонентами являются интегральные схемы, то, как правило, их задержки близки друг к другу в независимости от используемого компонента. Моделирование, в котором задержки всех элементов одинаковы, называются синхронными. Если задержки всех элементов разные, то моделирование – асинхронное. По длительности асинхронное моделирование занимает большое время, однако возможен анализ переходных процессов. Асинхронное моделирование более адекватное.
Схема, подлежащая моделированию, всегда проходит аранжировку, т.е. элементы схемы или компоненты располагаются на соответствующих уровнях. К первому уровню относятся элементы, входы которых связаны только с входными контактами. На 2-ом уровне располагаются элементы, входы которых связаны с входными контактами и элементами 1-ого уровня и т.д. На последнем уровне располагаются элементы, выходы которых связаны с выходными контактами схемы. При наличии обратных связей, обратные связи обрываются и схема ранжируется. Ранжирование необходимо для определения времени окончания моделирования. Наибольшее распространение получил табличный метод формирования выходных реакций.
В переходном процессе возможно появление состояния статических и динамических. В свою очередь они разделяются на 0-е и единичные.
0-е статические состязания предполагают, что в режиме устанавливается 0-е значение сигнала. А в переходящем процессе на короткое время возникает всплеск на единичное состояние. Динамическое состязание предполагает многократное изменение сигнала в переходящем процессе. Количество изменений нечетное и в уст. режиме значение сигнала различны.
В теории моделирования используются методы, способные выявить состязания, как статические, так и динамические еще до изготовления схемы.
Данная работа связана с методом Эхельбергера, который предложил работать с 3-мя и 5-ю алфавитами представления сигнала.
28.Методы выявления статических и динамических состязаний в цифровых схемах.
Выявление статических состязаний
Возможно появление состязаний при смене A и B.
A |
X1 |
X2 |
X3 |
C |
C1 |
C2 |
C3 |
B |
Y1 |
Y2 |
Y3 |
Эхельбергер предложил расположить между A и B набор C. Причем
Если на выходе любого элемента схемы в установившемся режиме получились одинаковые состояния 0 и 1, а на промежуточном наборе X, то на данном элементе возможно появление статических состязаний. Моделирование в 3-ззнаковом алфавите имеет определенные особенности и расширяет таблицу истинности любого элемента.
Каждый сигнал представляется алфавитом {0,1,X}. Рассмотрим элемент 2И-НЕ.
|
0 |
1 |
X |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
X |
X |
1 |
X |
X |
|
X1 |
X2 |
X3 |
1 |
2 |
3 |
A |
0 |
1 |
1 |
1 |
0 |
1 |
C |
X |
1 |
X |
X |
X |
X |
B |
1 |
1 |
0 |
0 |
1 |
1 |
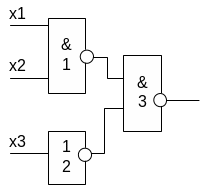
На выходе 3-го элемента возможно появление единицы – статических состязаний. Однако, данный метод не может выявить динамических состязаний, т.к. динамические состязания требуют знания фронтов сигнала. Для выявления динамических состязаний Эхельбергер предложил использовать пятиричный алфавит. {0,1,x,l,h}
l – фронт сигнала из 0 в 1.
h – фронт сигнала из 1 в 0
процедура выявления состязаний аналогична выше рассмотренной, причем на промежуточном наборе С формируется значение x,l,h. Если на 1-ом и 2-ом входных наборах значения сигнала на выходе элемента различны, а на промежуточном наборе значения x, то в схеме возможно появление динамических состязаний. Для реализации алгоритма необходимо переделать таблицу истинности к пятиричному алфавиту.
|
0 |
1 |
x |
l |
h |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
x |
h |
L |
x |
1 |
x |
x |
x |
x |
L |
1 |
h |
x |
h |
x |
h |
1 |
L |
x |
x |
L |
