4.2 Практическая проверка статистических гипотез о законах распределения случайных величин на основе конкретных данных
Рассмотрим случайную величину время появления клиента.
Таблица 1 – Значения времени появления клиента.
1 |
7 |
2 |
5 |
7 |
3 |
10 |
5 |
2 |
10 |
8 |
7 |
5 |
3 |
12 |
7 |
3 |
8 |
5 |
7 |
5 |
8 |
5 |
13 |
6 |
12 |
8 |
1 |
15 |
4 |
7 |
20 |
15 |
5 |
6 |
10 |
10 |
5 |
13 |
4 |
2 |
2 |
16 |
5 |
15 |
2 |
10 |
5 |
18 |
3 |
3 |
14 |
13 |
17 |
1 |
3 |
10 |
10 |
3 |
7 |
7 |
8 |
6 |
5 |
4 |
10 |
7 |
2 |
2 |
2 |
8 |
4 |
12 |
3 |
10 |
5 |
8 |
1 |
5 |
11 |
13 |
4 |
11 |
1 |
9 |
7 |
2 |
8 |
5 |
3 |
2 |
18 |
6 |
12 |
3 |
10 |
6 |
8 |
5 |
3 |
Разобьем выборку на 8 интервалов согласно формуле Стерджесса.
Таблица 2 - Эмпирическое распределение СВ и её числовые характеристики
Начало интер-вала Xi |
Конец интер-вала Xi+1 |
Часто-та Mi |
Час-тость Wi |
Центр интер-вала Xi cp |
Частота* центр интервала Mi*Xi cp |
Откло-нение от среднего Xi-Xcp |
Квадрат отклонения от среднего (Xi-Xcp)² |
Mi((Xi-Xcp)²) |
|
1 |
3,5 |
25 |
0,25 |
2,25 |
56,25 |
-10 |
100 |
2500 |
|
3,5 |
6 |
25 |
0,25 |
4,75 |
118,75 |
-7,5 |
56,25 |
1406,25 |
|
6 |
8,5 |
19 |
0,19 |
7,25 |
137,75 |
-5 |
25 |
475 |
|
8,5 |
11 |
13 |
0,13 |
9,75 |
126,75 |
-2,5 |
6,25 |
81,25 |
|
11 |
13,5 |
8 |
0,08 |
12,25 |
98 |
0 |
0 |
0 |
|
13,5 |
16 |
5 |
0,05 |
14,75 |
73,75 |
2,5 |
6,25 |
31,25 |
|
16 |
18,5 |
3 |
0,03 |
17,25 |
51,75 |
5 |
25 |
75 |
|
18,5 |
21 |
2 |
0,02 |
19,75 |
39,5 |
7,5 |
56,25 |
112,5 |
|
|
|
100 |
|
11 |
702,5 |
|
Дисперсия= |
46,8125 |
|
Построим гистограмму эмпирического распределения времени между клиентами.
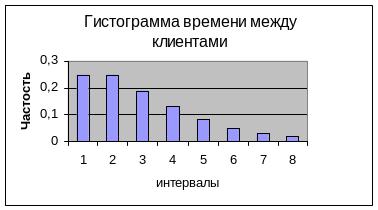
Рисунок 2 - Гистограмма эмпирического распределения.
Вид полученной гистограммы позволяет предположить, что исследуемая величина подчиняется показательному закону. λ= 1/х выб ср = 0,14235.
Таблица 3 - Вычисление теоретических вероятностей попадания в заданный интервал показательно распределенной случайной величины
-λ *Xi |
-λ *Xi+1 |
e-λ*хi |
e-λ*xi+1 |
Pi (вероятность) |
|
-0,142348754 |
-0,498220641 |
0,864995 |
0,601932 |
0,2630629 |
|
-0,498220641 |
-0,854092527 |
0,601932 |
0,418872 |
0,18306001 |
|
-0,854092527 |
-1,209964413 |
0,418872 |
0,291484 |
0,12738767 |
|
-1,209964413 |
-1,565836299 |
0,291484 |
0,202838 |
0,08864643 |
|
-1,565836299 |
-1,921708185 |
0,202838 |
0,141151 |
0,06168721 |
|
-1,921708185 |
-2,277580071 |
0,1411507 |
0,0982238 |
0,0429269 |
|
-2,277580071 |
-2,633451957 |
0,0982238 |
0,0683519 |
0,0298719 |
|
-2,633451957 |
-2,989323843 |
0,0683519 |
0,0475647 |
0,0207872 |
|
|
|
|
|
0,81743023 |
|
Таблица 4 - Вычисление наблюдаемого значения критерия
Pi |
n*Pi |
Mi-nPi |
(Mi-nPi)2 |
(Mi-nPi)²/n*Pi |
|
0,2630629 |
26,30629 |
-1,30629 |
1,706393 |
0,064866358 |
|
0,18306001 |
18,306 |
6,694 |
44,80962 |
2,447810213 |
|
0,12738767 |
12,73877 |
6,26123 |
39,20304 |
3,077459894 |
|
0,08864643 |
8,864643 |
4,13536 |
17,10117 |
1,92914403 |
|
0,06168721 |
6,168721 |
1,83128 |
3,353581 |
0,543642807 |
|
0,0429269 |
4,292685 |
0,70731 |
0,500294 |
0,116545716 |
|
0,0298719 |
2,987191 |
0,01281 |
0,000164 |
5,49277E-05 |
|
0,0207872 |
2,07872 |
-0,07872 |
0,006197 |
0,002981381 |
|
0,81743023 |
|
|
|
8,182505328 |
|
Таким образом,
расчетное значение
составляет
8,18. Критическое значение критерия при
уровне значимости = 0,05 и числе степеней
свободы = 6 равно 12,6. Так как
,
то нет оснований отвергнуть гипотезу
о показательном распределении времени
между клиентами.
Идентификация закона распределения является основой для проведения имитационного моделирования работы компании в будущем.
Стоит рассмотреть еще одну случайную величину, а именно случайное время разговора клиента.
Выборка из 100 значений аналогично разбивается на 8 интервалов.
Таблица 5 - Эмпирическое распределение СВ и её числовые характеристики
Начало интер-вала Xi |
Конец интер-вала Xi+1 |
Часто-та Mi |
Час-тость Wi |
Центр интер-вала Xi cp |
Частота* центр интер-вала Mi*Xi cp |
Откло-нение от сред-него Xi-Xcp |
Квадрат откло- нения от сред- него (Xi-Xcp)² |
Mi ((Xi-Xcp)²) |
|
2 |
5,75 |
28 |
0,28 |
3,875 |
108,5 |
-15 |
225 |
6300 |
|
5,75 |
9,5 |
23 |
0,23 |
7,625 |
175,375 |
-11,25 |
126,5625 |
2910,9375 |
|
9,5 |
13,25 |
17 |
0,17 |
11,375 |
193,375 |
-7,5 |
56,25 |
956,25 |
|
13,25 |
17 |
13 |
0,13 |
15,125 |
196,625 |
-3,75 |
14,0625 |
182,8125 |
|
17 |
20,75 |
8 |
0,08 |
18,875 |
151 |
0 |
0 |
0 |
|
20,75 |
24,5 |
6 |
0,06 |
22,625 |
135,75 |
3,75 |
14,0625 |
84,375 |
|
24,5 |
28,25 |
3 |
0,03 |
26,375 |
79,125 |
7,5 |
56,25 |
168,75 |
|
28,25 |
32 |
2 |
0,02 |
30,125 |
60,25 |
11,25 |
126,5625 |
253,125 |
|
|
|
100 |
|
17 |
1100 |
|
Дисперсия= |
108,5625 |
|
Построим график частости случайной величины.
Рисунок 3 - Гистограмма эмпирического распределения.
Вид полученной гистограммы позволяет предположить, что исследуемая величина подчиняется показательному закону. λ= 1/х выб ср =0,0909091.
Следующий этап – вычисление теоретических вероятностей попадания в интервал показательно распределенной случайной величины
Таблица 6 - Вычисление теоретических вероятностей попадания в заданный интервал показательно распределенной случайной величины
-λ*Xi |
-λ*Xi+1 |
e-λ*хi |
e-λ*xi+1 |
Pi |
-0,18181818 |
-0,522727273 |
0,83090072 |
0,5870887 |
0,243812 |
-0,52272727 |
-0,863636364 |
0,58708875 |
0,4148188 |
0,17227 |
-0,86363636 |
-1,204545455 |
0,41481875 |
0,2930981 |
0,121721 |
-1,20454545 |
-1,545454545 |
0,2930981 |
0,2070941 |
0,086004 |
-1,54545455 |
-1,886363636 |
0,20709405 |
0,146326 |
0,060768 |
-1,88636364 |
-2,227272727 |
0,1463263 |
0,1033896 |
0,0429366 |
-2,22727273 |
-2,568181818 |
0,1033896 |
0,0730519 |
0,0303377 |
-2,56818182 |
-2,909090909 |
0,0730519 |
0,0516162 |
0,0214357 |
Таблица 7 - Вычисление наблюдаемого значения критерия
Pi |
n*Pi |
Mi-nPi |
(Mi-nPi)² |
(Mi-nPi)²/n*Pi |
0,243812 |
24,3812 |
3,6188 |
13,0957 |
0,537124465 |
0,17227 |
17,227 |
5,773 |
33,3275 |
1,93461049 |
0,121721 |
12,1721 |
4,8279 |
23,309 |
1,914954864 |
0,086004 |
8,6004 |
4,3996 |
19,3564 |
2,250642706 |
0,060768 |
6,07678 |
1,9232 |
3,69878 |
0,60867352 |
0,0429366 |
4,29366 |
1,7063 |
2,91158 |
0,678110622 |
0,0303377 |
3,03377 |
-0,0338 |
0,00114 |
0,000375923 |
0,0214357 |
2,14357 |
-0,1436 |
0,02061 |
0,009615715 |
|
|
|
χ² |
7,934108305 |
Таким образом, расчетное значение составляет 7,93. Критическое значение критерия при уровне значимости = 0,05 и числе степеней свободы = 6 равно 12,6. Так как , то нет оснований отвергнуть гипотезу о показательном распределении времени разговора клиента.