§ 5. Вычисление объема тела

1. Вычисление объема тела по известным площадям поперечных сечений.

Если площадь сечения тела плоскостью, перпендикулярной оси Ох, может быть выражена как функция от х, т. е, в виде S = S(x), a≤x≤b_t то объем части тела, заключенной между перпендикулярными оси Ох плоскостями х = а и x = b, находится по формуле

2. Вычисление объема тела вращения. Если криволинейная трапеция, огра­ниченная кривой y = f(x) и прямыми y = 0, х = а, x = b, вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле

Если фигура, ограниченная кривыми y₁=f₁ (x) и y₂ = f₂(x) [0 ≤ f₁(x)≤f₂(x)| и прямыми х = а,

х = b, вращается вокруг оси Ох, то объем тела вращения

1626. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривой у² = (х— 1)³ и прямой х = 2 (рис. 43).

Рис. 43

Решение. Имеем

(куб. ед.)

1627. Найти объем тела, в основании которого лежит равнобед­ренный треугольник с высотой h и основанием а. Поперечное сече­ние тела есть сегмент параболы с хордой, равной высоте сегмента (рис. 44).

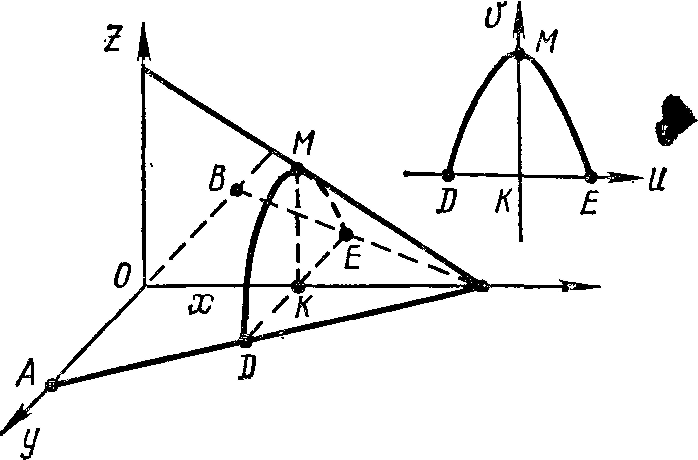
Рис. 44

Решение. Имеем |AВ| = a, |ОС| =h, |MK| = |DE|, |OK|=x. Выразим площадь поперечного сечения как функцию от х, для чего предварительно найдем уравнение параболы. Длину хорды DE можно найти из подобия соответствующих треугольников, а именно:

|DE|/a=(h-x)/h, т. е. |DE|=a(h-x)/h =|MK|

Положим |DE|=m, тогда уравнение параболы в системе координат uKv примет вид v= m-(4/m)u². Отсюда находим площадь поперечного сечения данного тела:

или

Таким образом,

Найти объемы тел, образованных вращением вокруг оси Ох фигур, ограниченных линиями:

1628.

1629.

1630.

1631.

1632. Найти объем тела, ограниченного плоскостями х = 1,х = 3, если площадь его поперечного сечения обратно пропорцио­нальна квадрату расстояния сечения от начала координат, а при х = 2 площадь сечения равна 27 (кв. ед.)

1633. Найти объем цилиндрического клина по его размерам, указанным на (задача Архимеда).

1634. В цилиндрический стакан с водой вложен параболоид вра­щения вершиной вниз. Основание и высота параболоида совпадают с основанием и высотой цилиндра. Найти объем оставшейся в ста­кане воды, если радиус основания равен r, а высота равна h.

§ 6. Вычисление площади поверхности вращения

Если дуга гладкой кривой у = f (х) (а≤х≤b) вращается вокруг оси Ox, то площадь поверхности вращения вычисляется по формуле

. Если кривая задана параметрическими уравнениями х = х(t), y =(t), (t₁≤t≤t₂)

то

1635. Найти площадь поверхности, образованной вращением вокруг оси Ох дуги синусоиды у= sin2x от х = 0 до х = π/2.

Решение. Находим y' = 2 cos 2x; тогда

Произведем замену переменной: 2соs2x=t, — 4 sin 2x dx = dt, sin2xdx = (— 1/4) dt. Найдем пределы интегрирования по t: если х=0, то t = 2; если х = π /2, то t = — 2. Таким образом,

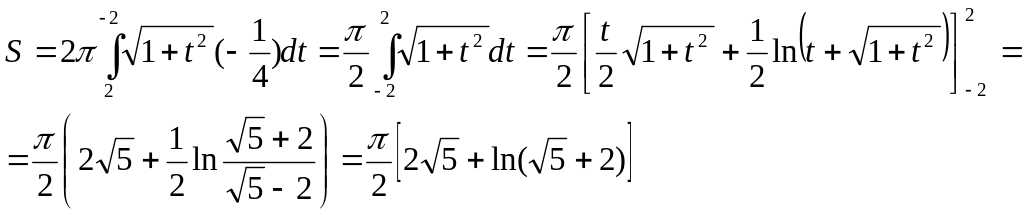(кв. ед.).

Найти площади поверхностей, образованных вращением вокруг оси Ох дуг кривых:

1636. y = 2ch(x/2) от x = 0 до x = 2.

1637. у = х³ от x = 0 до х=1/2.

1638. х²/ a² + y² /a² =1

1639. x = t — sin t, у=1— cost (площадь, образованную враще­нием одной арки).